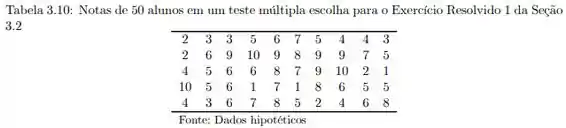
Considere novamente as notas dos 50 alunos, reproduzidas na Tabela 3.10. Calcule o intervalo interquartil das notas.
Passo 1
Primeiro temos que colocar esses dados em ordem, mas como tem muiiito dado pra gente reescrever, vamos usar aquele conceito de frequência para representá-los:
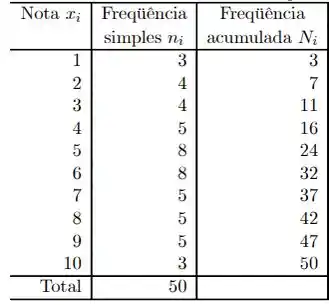
Nós escrevemos todos os valores de notas que aparecem nos dados e ao lado representamos a frequência simples de cada um, ou seja, quantas vezes cada um aparece. A última coluna, de frequência é simplesmente a frequência simples do analisado somada a todas as frequências simples anteriores.
Ok, voltando a questão, para calcular a distância interquartil temos que lembrar que:
Vamos começar calculando , nosso terceiro quartil. Ele deve estar na posição:
Onde é o número total de dados. No nosso caso :
Temos que fazer uma média ponderada entre o e o dado da tabela.
Olhando nossa tabela de freqüências, temos que procurar onde está o os dados e nas freqüências acumuladas.
Podemos observar que a frequência acumulada se torna para , então quanto terminamos de contar todas as notas até o temos dados. Então o dado vai ser e é o dado que temos imediatamente após o , já que é o último , ou seja, o dado é o .
Fazendo a média interpolada para , estamos mais perto do º (que vale )e mais perto do (que vale ), então:
Mas repara comigo, nessa tabela a gente só tem números inteiros, o valor nem existe nela. Então para tudo fazer mais sentido, vamos considerar que o terceiro quartil é isso aí arredondado mesmo:
Passo 2
Agora o primeiro quartil, a posição dele é dada por:
Mas olhando na tabela vemos que tanto o como o dado valem . Então de cara podemos afirmar que:
Portanto nossa é: