Determine o volume do sólido em cada um dos seguintes casos:
c) é a região do primeiro octante limitada pelo cilindro e pelo plano .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume do sólido que é limitadono primeiro octante pelo cilindro e pelo plano . Plotando esse cilindro junto com o plano, nós temos:
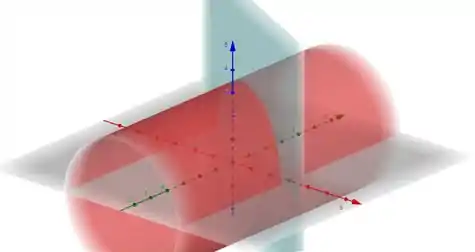
Mas a gente quer só a parte positiva desse sólido, que tá no primeiro octante. Repare que no plano , nesse caso, a projeção do sólido é a reta (é só isolar na equação do plano). Então, a gente vai prestar atenção em como as variáveis , e estão variando, ou seja, em como elas são limitadas nessa região (na projeção e no espaço tridimensional). Com isso em mente, a gente consegue encontrar os limites de integração do nosso volume na equação:
Vamos lá!
Passo 2
Repare que em , nosso sólido varia conforme a altura do cilindro. Sendo assim, isolando na equação do cilindro, temos , ou seja:
No plano , vamos ter:
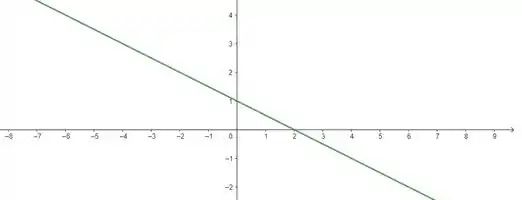
Assim, observe que o vai de até . E o varia de até a reta . Então, vamos ter:
Passo 3
Agora que já temos nossos intervalos, é só montar a integral de volume:
Integrando primeiro em relação a , temos:
Integrando agora em relação a :
Aplicando os limites de integração em :
Passo 4
Pra integrar em relação a , vamos separar a subtração em duas integrais:
Assim, vamos precisar usar métodos diferentes em cada integral. Na primeira integral, usando a substituição trigonométrica, vamos fazer , de modo que:
Além disso, quando , temos e quando , temos . Substituindo tudo, vai ficar:
Usando a identidade , temos:
Agora vamos usar outra relação trigonométrica :
Assim, integrando, vamos ter:
Aplicando os intervalos de integração:
Passo 5
Pra segunda parte da integral do volume, , vamos usar uma substituição simples, fazendo e
Além disso, quando , temos e quando , temos . Assim, vamos ter:
Como temos um limite inferior maior do que o limites superior, a gente pode inverter o intervalo trocando o sinal da integral:
Integrando em relação a e aplicando os intervalos:
Substraindo nossos resultados na equação:
Temos nosso volume:
Valeu, galera! Até a próxima! 😉