Teoria
Erros Absolutos e Relativos

Fala meus queridos, tudo certinho? Vamos relembrar um pouquinho uma teoria que é fundamental pro encaminhamento das ciências exatas. Principalmente quando fazemos o comparativo de experimentos e teorias! Adivinhe só qual é? ERROS!
Nós começamos entendendo um pouco sobre como máquinas funcionam e como os erros costumam aparecer, vamos pro objetivo dessa nossa conversinha. Estudar os erros de verdade!
O Erro numérico costuma ser a diferença entre o valor verdadeiro e uma aproximação, recebendo o nome de Erro Absoluto.
Nesse caso, é o valor verdadeiro e é o valor aproximado.
Geralmente nós não conhecemos o valor exato do que estamos querendo aproximar. Nesse caso, é impossível obtermos o valor exato do erro absoluto. A solução então é encontrar um limitante superior ou uma estimativa para o erro.
Veja bem, sabemos que está entre . Então tomando como um valor qualquer dentro desse intervalo temos garantidamente que:
Imagine agora que temos um número representado por . E um número representado por . Em ambos os casos temos o mesmo limitante superior para o erro:
Hmm... certo. Será que podemos afirmar que a precisão é a mesma? Vamos usar um exemplo literal pra ficar mais claro. Pensa assim, o que é pior, você errar por a medida da altura de um prédio ou errar por a medida da largura de um caderno?
Poxa vida, errar em a medida da largura de um caderno?! Isso é muita coisa né? Errar 10 cm em um caderno é quase como errar o tamanho dele como um todo. Mas, o que são na altura de um prédio gigantesco? é insignificante. Quando comparamos a ordem de grandeza das coisas fica fácil, mas como fazer isso matematicamente?
Mas agora imagine, uma indústria de papel e celulose, vai preparar papéis para encadernar e erra acidentalmente 10 de toooooooooooooooooooooooodo aquele material.

Concorda comigo que é um baita de um prejuízo? Então o PROBLEMA principal desse método é que ele NÃO LEVA EM CONTA A GRANDEZA!!!!!
E é aaaaaaaaaaí que entra o nosso Erro Relativo! Ele é a relação entre o erro absoluto e o valor exato.
No entanto, como muitas vezes não temos o valor exato, é possível usarmos a aproximação no denominador. Encontrando o erro relativo daqueles exemplos, temos, aí por via de regra você pode usar o valor aproximado sem peso na consciência:
No dia a dia da vida real, geralmente representarmos o erro relativo como uma porcentagem. Dessa forma, os exemplos acima ficariam:
Está mais que confirmado então que o número está sendo representado com precisão bem maior que o . Ou seja, dependendo da ordem de grandeza dos números envolvidos, o erro absoluto não é suficiente para julgarmos a precisão de uma medida ou um cálculo.
Erros de Arredondamento e Truncamento em um Sistema de Aritmética de Ponto Flutuante
Deu pra dar uma relembrada boa em erros? Ótimo!!!! Então segue o jogo.
No tópico sobre aritmética de ponto flutuante vimos como as máquinas representam os números, vimos também que há um limite de que podem ser representados na mantissa. Isso significa que existe um limite de precisão que o sistema pode representar.
Veja esse exemplo: em um sistema na base () com dígitos na mantissa ( 5), como ficaria a representação do número ?
Hmmmmm..., mas ele não pode ser apresentado assim né? Cabem só 5 dígitos na mantissa, então temos duas opões: arredondamento ou truncamento:
Seria representado como caso optássemos pelo arredondamento ou como caso o sistema usasse o truncamento. Existe algum erro envolvido??? Com toda certeza, lembra do que falamos em algarismos significativos sempre haverá um número duvidoso e nele incide o erro. Por isso é meeeeeega importante que você faça o arrendondamento correto, para evitar o agravamento desses erros.
Para o arredondamento teríamos:
E para o truncamento:
Como vimos, o arredondamento gera erros menores, mas exige um tempo maior de execução. Em geral, seja o expoente do número em sua representação normalizada em ponto flutuante e o número de na mantissa, temos como limitantes para o erro por truncamento:
No nosso exemplo temos e , logo:
Já para o arredondamento, temos como limitantes:
No nosso exemplo,
Comprovando mais uma vez que o arredondamento acarreta erros menores.
Erros nas Operações Aritméticas de Ponto Flutuante
Quando falamos em erros, eles podem estar presentes em diversas esferas. Veja bem, a maior parte dos estudos científicos, experimentais, projetos estão propensos a erro em algum momento.
Geralmente pensamos no erro humano que é o mais normal, que pode estar em medidas erradas, erros em experimento, perda de material e etc. Em laboratório, alguns equipamentos marcam a quantidade de erros que eles podem gerar. Somando isso, a representação errada de números... eh, a lista aumenta cada vez mais. E é por isso, que esse assunto é bem importante.
Mas as máquinas também erram ok? Então não fique triste!
Além daqueles erros na representação de números (que acontecem por conta de arredondamento, quantidade de números na mantissa que já conversamos) ...
As operações aritméticas feitas por um computador não são exatas e também contém erro!!! Vamos ver um exemplo para ficar mais claro.
Imagine um sistema de aritmética de ponto flutuante de cinco dígitos, na base . Suponha e . Usando truncamento para calcular , , e nós teríamos:
A representação no sistema ficaria:
Sendo assim:
Os erros de cada operação seriam:

Pra minimizar isso existem algumas técnicas que ajudam a reduzir bastante os erros incumbidos nessas operações.
Mas, espera aí... não é só somar e subtrair ?????????
Nãaaaaaaaaaaaaaaaaaao.
Vamos dar uma olhadinha aqui. A primeira regra é que a ADIÇÃO E SUBTRAÇÃO na aritmética de ponto flutuante requer o alinhamento dos pontos decimais dos dois números. Beleza, mas o que isso significa? Basicamente a mantissa do número de menor expoente deve ser deslocada para direita até que a base decimal seja a mesma. Vamos ver como fica?
Seja e , efetue a operação . Vamos lá!
Você provavelmente pensou assim né:
Mas na aritmética de ponto flutuante nós devemos respeitar as regras e transformar todo mundo em base decimal!
Tá melhorando, o que falta agora? Isso mesmo, igualar a base do número de menor expoente ao número de maior expoente:
Basicamente nós enchemos de zeros a esquerda até chegar em .
Utilizando precisão dupla, ou seja, aqui nós usamos a representação com , mas fazemos os cálculos com . Só mudamos na hora de dar o resultado final utilizando arredondamento ou truncamento, assim nós minimizamos a tal da propagação de erro.
Fazendo arredondamento:
Com truncamento:
Nós não podemos representar deforma exata nesse sistema, mas podemos usar a mais próxima do valor real o arredondamento.
Mas e no caso de MULTIPLICAÇÃO e DIVISÃO? Nesse caso o processo é até mais fácil, nós só utilizamos propriedades de potência. Veja bem, primeiro transformamos todo mundo em base 10. Até aí tudo bem... aí nós separamos as operações em (base)*(mantissa) . Parece complicado, mas você vai ver que é até mais fácil, vamos usar o exemplo anterior!
Seja e , efetue a operação . Vamos lá!
Mas na aritmética de ponto flutuante nós devemos respeitar as regras e transformar todo mundo em base decimal!
Tá melhorando, o que falta agora? Unir as mantissas e unir os expoentes:
Multiplicar as mantissas é fácil né? os expoentes também! Tem uma propriedade de potência que envolve multiplicação de expoentes diferentes e bases iguais: Repete a base e soma os expoentes (tem toda uma explicação matemática encima disso, mas pro que queremos essa explicação já basta).
Agora é só colocar representar corretamente os algarismos com :
No arredondamento:
No truncamento:
Molezinha né? Terminamos por aqui!
#PartiuExercícios
Erros de Arredondamento e Truncamento em um Sistema de Aritmética de Ponto Flutuante
Erros nas Operações Aritméticas de Ponto Flutuante
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de Darezzo, S.A.|. A. Cálculo Numérico: aprendizagem com Apoio de Software.
Consideremos o valor exato e aproximado de um determinado número.
- Calcule o Erro Absoluto e Erro Relativo para os valores dados acima.
- Consideremos o valor exato e valor aproximado
Passo 1
- Calcule o Erro Absoluto e Erro Relativo para os valores dados acima.
- Consideremos o valor exato e valor aproximado
Vamos lá, as fórmulas de Erros Absoluto e Relativo nos perseguem deeeeeeeeesde a Física 1, mas acredite, são fórmulas bem importantes pra vida real e nos impedem de cometer erros grotescos que podem derrubar uma ponte heheh
Então, espero do fundo do meu coração que você guarde essas fórmulas com muito carinho .
Vamos lá, começamos pelo Erro Absoluto:
É só substituir os valores:
E no caso do Erro Relativo?
Hmmmmm... que eu faço mesmo? Sim amigo, só substituímos:
Geralmente o Erro Relativo é dado em termos percentuais e pode ser escrito assim:
Viu só, nem gastamos muitos neurônios aqui e ainda da tempo de fazer um lanchinho!
Passo 2
Agora veja bem, vamos fazer exatamente o que fizemos lá encima né?
É só substituir os valores:
Perceba que esse erro absoluto deu exatamente o mesmo para os dois casos.E no caso do Erro Relativo?
Hmmmmm... que eu faço mesmo? Sim amigo, só substituímos:
Geralmente o Erro Relativo é dado em termos percentuais e pode ser escrito assim:
Espera aí... Os erros absolutos ficaram iguais já que a diferença entre os dois termos é a mesma... mas a proporção não é considerada no Erro Absoluto.
Aí é que entra o Erro Relativo, ele considera a proporção: tipo assim, perceba que no segundo o carro o Erro Relativo foi beeeeeeeeeeeeeem maior. Considere assim, quanto menor for a escala considerada, maior será o erro!
Resposta
- ; .
- ; .
Exercício Resolvido #2
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 28, exercício 2.
Encontre o maior intervalo para no qual deve estar para aproximar com erro relativo de no máximo para cada favor de .
Passo 1
Queremos um erro relativo de no máximo . Ou seja, queremos , tal que:
Passo 2
O maior intervalo será então:
Ou, aproximadamente:
Conseguiu ver o padrão? O intervalo vai ser sempre dado por !
Passo 3
Passo 4
Passo 5
Resposta
Exercício Resolvido #3
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 29, exercício 10.
O número pode ser definido por
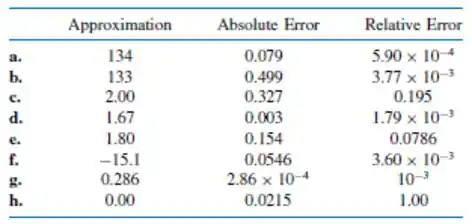
onde para e . Calcule o erro absoluto e relativo das seguintes aproximações de :
Passo 1
Bom, sabemos que o Erro Absoluto é a diferença entre o valor verdadeiro e a aproximação:
Onde é o valor verdadeiro e a aproximação.
Já o Erro Relativo é a relação entre o Erro Absoluto e o valor verdadeiro:
Nesse caso nosso valor real é o próprio número e a aproximação é dada pelo enunciado.
Já relembramos o que precisamos para resolver o item (a)
Vamos abrir o somatório para descobrir o valor da aproximação:
Resolvendo os fatoriais temos:
Calculando o Erro Absoluto:
Agora o Erro Relativo:
Passo 2
Vamos fazer a mesma coisa para o item (b)
Vamos abrir o somatório para descobrir o valor da aproximação:
Utilizando uma calculadora chegamos no seguinte valor:
Calculando o Erro Absoluto:
Agora o Erro Relativo:
Resposta
Exercício Resolvido #4
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 28, exercício 5.
Usando um sistema de aritmética de ponto flutuante de dígitos que utiliza arredondamento, faça os cálculos abaixo. Em seguida, calcule o erro absoluto e relativo de cada operação com pelo menos dígitos.
Passo 1
Passo 2
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Passo 8
Resposta
Exercício Resolvido #5
Lista 1 – Professora Angela – UFRJ – Questão 8
Seja uma máquina de base decimal com aritmética de ponto flutuante normalizado com dígitos para a mantissa e dígito para a característica. Para calcular a média aritmética dos números e nesta máquina é mais conveniente calcular ou ? Justifique.
Passo 1
Primeiramente repare que aqui estamos na base decimal! A parte importante aqui é que temos apenas dígito para a característica, que é o expoente! Ou seja, só podemos representar expoentes de a ! Se somarmos os números antes da divisão, teremos:
Opa, apareceu um expoente , ta vendo? Isso não poderia acontecer! Então é mais conveniente dividirmos antes de somarmos evitando esse problema:
Resposta
Pois assim evitaríamos o expoente que é não pode ser representado com apenas dígito para a característica.
Exercício Resolvido #6
Lista 1 – Professora Angela – UFRJ – Questão 6
Supondo que as operações abaixo sejam processadas em uma máquina de base decimal com dígitos na mantissa e tomando e calcule usando arredondamento:
Analisando e o que se pode concluir em relação à propriedade associativa da adição em aritmética de ponto flutuante?
Passo 1
Passo 2
Passo 3
Analisando os resultados obtidos podemos concluir que a propriedade associativa não é sempre válida na adição em aritmética de ponto flutuante.
Resposta
Analisando os resultados obtidos podemos concluir que a propriedade associativa não é sempre válida na adição em aritmética de ponto flutuante.
Exercício Resolvido #7
Adaptado da lista de exercícios de Cálculo Numérico: Integração Numérica - UniVap - Exercício 1
Seja um sistema em aritmética de ponto flutuante de quatro dígitos, base decimal e com acumulador de precisão dupla. Dados os números: 𝑥 = 0,7237 × 104 , 𝑦 = 0,2145 × 10−3 , 𝑧 = 0,2585 × 101 .Efetue as seguintes operações, considere arredondamento e calcule o erro envolvido.
(a)
(b)
(c)
d)
Passo 1
(a)
Se : 𝑥 = 0,7237 × 104 , 𝑦 = 0,2145 × 10−3 , 𝑧 = 0,2585 × 101 ;
A adição e alinhamento na aritmética de ponto flutuante requer alinhamento dos pontos decimais de todos os números envolvidos!
Mas, como fazemos isso?
A mantissa dos termos com menor expoente deve ser colocado na mesma base e expoente que o termo de maior expoente. Confuso? Basicamente, o menor expoente vai ser deslocado para direita .
Agora vamos lá, o que ta faltando? Issooooo mexxxxmoooo! Vamos alinhar todos os termos e mantissa!
De boa né?
Qual o erro envolvido?
Passo 2
(b)
Se : 𝑥 = 0,7237 × 104 , 𝑦 = 0,2145 × 10−3 , 𝑧 = 0,2585 × 101 ;
Vamos fazer o quê??? Isso mesmo, alinhamento da mantissa!
A mantissa dos termos com menor expoente deve ser colocado na mesma base e expoente que o termo de maior expoente.
Agora vamos lá, o que ta faltando? Issooooo mexxxxmoooo! Vamos alinhar todos os termos e mantissa!
Só isso, moleza né?
Passo 3
(c)
Se : 𝑥 = 0,7237 × 104 , 𝑦 = 0,2145 × 10−3 , 𝑧 = 0,2585 × 101 ;
Bora montar a divisão!
Vamos fazer o quê??? Isso mesmo, alinhamento da mantissa!
Boaaaa ! Bora fazer o último que você ta quase craque!
Passo 4
d)
Se : 𝑥 = 0,7237 × 104 , 𝑦 = 0,2145 × 10−3 , 𝑧 = 0,2585 × 101 ;
Bora montar a divisão!
Vamos montar o alinhamento da mantissa!
Show de bola!!
Resposta
(a)
(b)
(c)
d)
Exercício Resolvido #8
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 23, exercício 9 adaptada.
Considere uma máquina cujo sistema de representação de números é definido por: , , e . Pede-se:
Se e qual o resultado de ?
Qual o resultado da soma
nesta máquina?
Idem para a soma:
Passo 1
Passo 2
Repare que sabemos que o resultado da soma nessa máquina vale . Então cada vez que somamos individualmente o ao ele vai sumindo devido à precisão limitada da máquina, de modo que:
Passo 3
Agora ao invés de somarmos os individualmente no , nós vamos soma-los entre si e depois adicionamos ao :
Resposta
Exercício Resolvido #9
Lista 1 – Professor Daniel – UFRJ – Questão 3 Adaptada
Considere uma máquina com sistema de representação de números definido por: base , precisão de dígitos na mantissa e expoente no intervalo: . Pede-se:
Qual o menor e o maior número em módulo representáveis nesta máquina?
Como será representado o número nesta máquina se for usado o arredondamento? E o truncamento?
Se e qual o resultado de se for usado o arredondamento? E se for usado o truncamento?
Considerando a letra acima, qual o resultado da operação , considerando que está sendo realizado o truncamento?
Repetir o item , para a operação .
Passo 1
A máquina funciona na base decimal com dígitos na mantissa e expoente indo de até . Então, o maior número será:
E o menor número:
Passo 2
Usando o arredondamento:
Usando o truncamento:
Passo 3
Usando o arredondamento:
Usando o truncamento:
Passo 4
Agora nós somaremos várias parcelas dos 0.6 e depois somaremos isso aos 257820:
Passo 5
Usando o truncamento nós vimos que a soma individual de . Se fizermos essa soma vezes, o resultado continuará sendo o mesmo:
Resposta
Maior número:
Menor número:
Usando o arredondamento:
Usando o truncamento:
Usando o arredondamento:
Usando o truncamento:
Exercício Resolvido #10
Lista 1 – Professor Raymundo – UFRJ – Questão 3 e 8 Adaptada
Um computador armazena números reais em binário utilizando para o sinal do número, para o expoente e para a mantissa. Admitindo que haja truncamento, quais os erros absoluto e relativo ao se tentar nele representar os números:
Passo 1
Os do expoente variarão de até , isto é, de até . Como precisamos representar expoentes negativos, subtraímos disso de modo que o expoente agora varie de até .
Passo 2
Agora temos que passar nos números para binário e ver qual vai ser o erro:
Logo,
Representando na máquina:
Não perdemos nenhuma casa decimal então não houve erro.
Passo 3
Logo,
Representando na máquina:
Não perdemos nenhuma casa decimal então não houve erro.
Passo 4
Representando na máquina:
Não perdemos nenhuma casa decimal então não houve erro.
Passo 5
Logo,
Representando na máquina:
No final das contas representamos apenas o , então o erro absoluto foi de:
E o relativo:
Passo 6
Logo,
Representando na máquina:
No final das contas representamos apenas o , então o erro absoluto foi de:
E o relativo:
Resposta
Nenhum erro.
Nenhum erro.
Nenhum erro.
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais
Ver Mais
Ver Mais