1 ) Utilizando o teorema de Stokes, transforme a integral
numa integral de linha e calcule.
sendo a normal apontando para cima
Passo 1
Antes de Começarmos temos que lembrar como é o teorema de Stolkes
OU seja podemos igualar ao fluxo que atravessa uma superfície pelo trabalho da força ao percorrer a borda. Com isso conseguimos reduzir o problema de 2 variáveis, em apenas 1. E lembrando que ainda podemos usar parametrizações para isso. Assim ficamos com
E com isso conseguimos resolver todos os nossos problemas.
Passo 2
O grande problema são as parametrizações. Porque temos essa superficie
Geometricamente temos
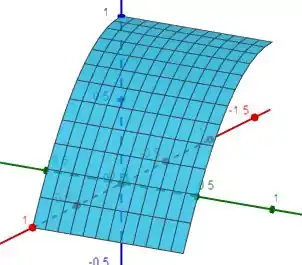
Com a seguinte limitação
OU seja ficamos com
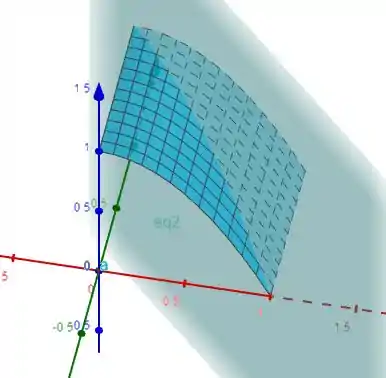
A parte interna não hachurada dessa superficie. E temos que parametrizar para ter as curvas nos eixos ortogonais X , Y, além de a curva em preto que fecha nosso contorno
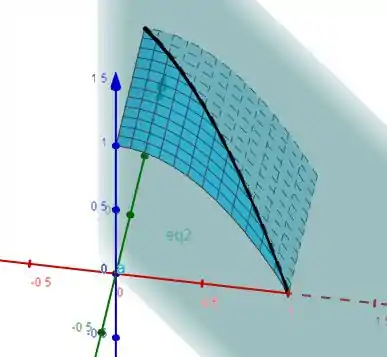
Vamos cair dentro então . Temos que criar 3 parametrizações para essas 3 curvas em preto
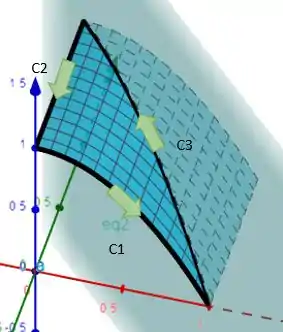
Visto que estamos na parábola
Já C2 será
E por fim o C3
Visto que a curva C3 é a interseção de
Essa é uma parametrização mais difícil de enxergar. Uma dica é entrar no site do geogebra 3d e ir testando suas hipóteses de parametrização durante os exercícios ate ficar afiado 😉.
Vamos continuar. Temos que nossa função é
Agora vamos calcular as integrais de linha
Passo 3
Terminamos por aqui. Te vejo na próxima resolução
: )