Corpos Rígidos, Momento Angular
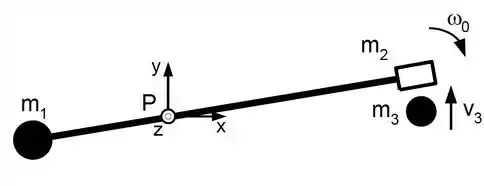
A figura mostra uma montagem de laboratório utilizada para experiências de momento angular. Ela é composta por 3 corpos: i) uma haste fina de massa e comprimento articulada por um eixo sem atrito (localizado no ponto P) distante de uma de suas extremidades; ii) uma pequena esfera sólida de massa , presa à extremidade mais próxima ao eixo da haste e iii) um aro de raio e massa preso à outra extremidade. A montagem está girando no plano horizontal com velocidade angular (no sentido horário), quando sofre uma colisão ao se encontrar na posição à acima do eixo com uma esfera sólida de massa que se move com velocidade . A esfera fica presa no aro.
Considere as esferas como pontuais. Utilize: ; .
Calcule o momento de inérica de cada componente da montagem em torno do ponto P, formado pela haste fina, esfera de massa e aro.
Calcule o vetor momento angular total do sistema imediatamente antes da colisão (. Responda se haverá ou não conservação do momento angular do conjunto durante a colisão, justificando cuidadosamente.
Calcule o módulo da velocidade angular imediatamente após a colisão e informe também o sentido da rotação do conjunto.
Passo 1
Para o item , devemos calcular o momento de inércia de cada componente, lembrando que , além de recordar o teorema dos eixos paralelos .
Para a esfera de massa , que está à do ponto , temos:
Para o Aro de massa e raio , que está a do ponto , temos:
Para a haste de massa e comprimento , temos:
É a distância entre o da barra e o ponto .
Passo 2
Agora podemos calcular o item . Para isso, vamos relembrar a definição de momento angular: , onde é o momento linear, além de recordar o momento angular de corpos rígidos, dado por . Agora sim, podemos calcular o momento angular total do sistema antes da colisão.
Passo 3
Vamos primeiro calcular o momento angular referente aos componentes do corpo rígido. Nessa parte da equação é só copiar e colar, pois temos os momentos de inérica, já calculados no item , e sabemos também a velocidade angular .
Passo 4
Agora vamos calcular o momento angular da esfera de massa. No momento da colisão, sabemos que a esfera está com uma velocidade e que estará à mesma distância do ponto que está o aro, ou seja . Com isso, temos:
Passo 5
Portanto, o momento angular total, antes da colisão será:
Como consideramos parte do sistema, todas os componentes, e calculamos o momento angular com isso em mente, durante a colisão nenhum torque externo age sobre o sistema, desse modo haverá sim a conservação do momento angular total do conjunto durante a colisão.
Passo 6
Para encontrar a velocidade angular após a colisão, iremos recorrer justamente à conservação do momento angular.
Como já calculamos o momento de inércia dos três primeiros componentes. Precisamos agora calcular o momento de inércia da esfera que ficou presa no aro.
Passo 7
Podemos calcular o momento de inércia da esfera, assim como calculamos no item , se liga! Ah...lembra que a esfera estará àquela mesma distância do ponto . Ficou super fácil!
Passo 8
Agora sim podemos terminar. Voltando à equação de conservação do momento angular, temos:
sentido anti-horário! É só usar a regra da mão direita!
Resposta