Uma pistola de brinquedo dispara bolinhas plásticas utilizando um gatilho externo para movimentar uma mola de constante que se encontra em seu compartimento interno. Uma vez inserida uma bola de massa num extremo da mola, se aperta o gatilho produzindo uma compressão de na mola. Quando o gatilho é apertado até o limite, a mola volta à posição inicial imediatamente e a bolinha é solta adquirindo uma velocidade.
Considere as afirmativas:
I Quanto maior é a compressão da mola maior a velocidade adquirida pela bola.
II A velocidade com que a bola abandona a pistola depende de , e .
III Usando a mesma pistola, mas, trocando a bola plástica por uma bola de aço de igual tamanho e massa maior, a velocidade depois do disparo seria a mesma.
São verdadeiras:
(a) Apenas a I e a II
(b) Apenas a II.
(c) Apenas a III.
(d) Apenas a I.
(e) Nenhuma.
Passo 1
Fala galera do fundão! Bora matar essa questãozinha juntos?

Primeiro, vamos fazer um desenho do que tá acontecendo...
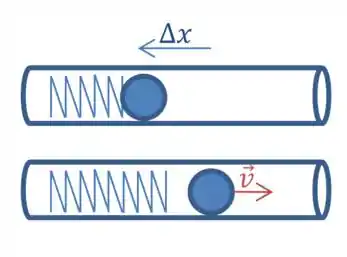
Inicialmente, temos uma bolinha que está comprimindo uma mola no interior de uma arma de brinquedo. A compressão que essa bolinha faz na mola é de um comprimento .
Após liberar a bolinha, a mola se descomprime e a bola adquire uma velocidade .
Essa é a velocidade com que a bolinha sai da arma de brinquedo, ou seja, sua velocidade de lançamento, pois não há atrito.
Podemos conservar a energia nessa movimentação, fazendo energia mecânica inicial é igual a final.
No início, a bola comprime a mola e ela está em repouso, portanto, haverá uma energia potencial elástica e não há energia cinética.
No final, a bola possui uma velocidade e a mola está relaxada.
Dessa forma, teremos:
Passo 2
Vamos avaliar cada uma das afirmativas.
I Quanto maior é a compressão da mola maior a velocidade adquirida pela bola.
De fato, podemos ver pela última equação do passo 1 que a velocidade de lançamento é diretamente proporcional com , por conta disso, é verdade que quanto maior a compressão, maior a velocidade.
Passo 3
II A velocidade com que a bola abandona a pistola depende de , e .
Bom, se resolvermos a última equação do Passo 1 para , teremos:
E é verdade, a velocidade de lançamento depende dessas três grandezas.
Passo 4
III Usando a mesma pistola, mas, trocando a bola plástica por uma bola de aço de igual tamanho e massa maior, a velocidade depois do disparo seria a mesma.
Bom... temos que tomar cuidado aqui... ao usar a mesma pistola, você vai ter o mesmo que é a constante elástica. Não se fala nada sobre , mas acredita-se que se faria a mesma compressão, então é o mesmo.
O fato da bola agora ser de aço, não interfere em nada. Afinal, estamos desconsiderando atritos.
Mas a massa é maior... e olhando para a nossa expressão da velocidade que eu acabei de encontrar no passo 3, vemos que:
Ou seja, a velocidade é inversamente proporcional com a massa... Portanto, como a massa aumenta, a velocidade diminui, daí essa afirmativa está errada.
A resposta correta é a letra a).
Resposta
Letra a)