Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica

Ver Teoria
Exercício 541234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253555657585960616263646566

Enunciado

Fundamentos de Física – Halliday e Resnick. 9° Ed. Volume 1. Seção 8.5, Questão 34.

Um menino está inicialmente sentado no alto de um monte hemisférico de gelo de raio R = 13,8   m . Ele começa a deslizar para baixo com uma velocidade inicial tão pequena que pode ser desprezada (Fig. 8-45). Suponha que o atrito com o gelo seja desprezível. Em que altura o menino perde contato com o gelo?

Figura 8-45 Problema 34

Passo 1

Tomemos como referência para a energia potencial a base do monte

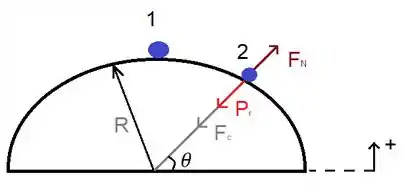
No ponto 1 temos energia potencial gravitacional dada por

U 1 = m g R

E no ponto 2, temos energia cinética e potencial gravitacional

U 2 = m g R s e n θ + m v 2 2

Passo 2

A resultante das forças que atuam na direção do raio é denominada Força centrípeta e dada por

F r = F c

P s e n θ - F N = m v 2 R

Em 2, perde-se o contato com o monte de gelo, logo

F N = 0

O que dá

m v 2 R = m g s e n θ

Colocando v 2 em evidência

v 2 = g R s e n θ

Passo 3

Pela lei da conservação de energia entre o ponto 1 e 2

U 1 = K 2 + U 2

m g R = m g R s e n θ + m v 2 2

g R = g R s e n θ + m v 2 2

v 2 2 = g R 1 - s e n θ

Substituindo v 2

g R s e n θ = 2 g R 1 - s e n θ

s e n θ = 2 - 2 s e n θ

3 s e n θ = 2

s e n θ = 2 3

Passo 4

Logo, a altura h será

s e n θ = h R

h = R s e n θ

h = 2.13,8 3

h = 9,2   m  

Resposta

h = 9,2   m  

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Em uma erupção vulcânica, um pedaço de 2k g de um rocha vulcânica porosa é jogada diretamente para cima com uma rapidez inicial de 40m / s . Ela viaja por uma distância de 50m antes de começar a cair