Um pêndulo simples é constituído de uma massa de m = 1 kg suspensa por um fio de comprimento L com massa desprezível.
(a) [1,0] Escreva as equações de movimento para um ângulo de desvio em relação à posição de equilíbrio, justificando sua resposta. Supondo que o pêndulo execute pequenas oscilações em torno da posição de equilíbrio:
(b) [1,0] Determine o comprimento para que o período de oscilação seja de s.
(c) [1,0] Mostre que a energia total do pêndulo é constante.
Passo 1
a) Dá uma olhada nessa imagem aqui:
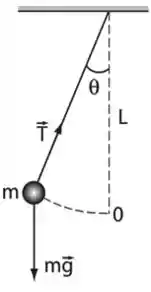
Ela tá mostrando o diagrama de corpo livre desse cara, e todas as forças que tão atuando nele. Essa força peso vai se decompor em uma parte paralela à tensão no fio (radial) e em uma parte paralela ao movimento (tangencial). Então vai ficar assim:
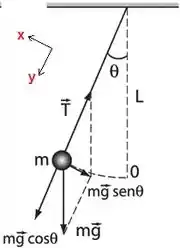
Repara ali que eu adotei dois eixos: x, paralelo ao movimento, com sentido positivo pra esquerda; y, paralelo ao fio, com sentido positivo pra baixo.
Aplicando a segunda lei de Newton aí nesse carinha, na direção radial (eixo y) vai ficar:
E na direção tangencial:
Eu coloquei os sinais das forças de acordo com os eixos que eu adotei! Na prática, isso não faz diferença. Você só tem que ser consistente na distribuição das forças e na aplicação da segunda lei.
Passo 2
As equações que nós temos para os dois eixos são:
No eixo y não tem movimento (a bolinha não se move paralela ao fio). Então a aceleração vai ser zero!
Show! O único eixo que vai ter movimento será o x. Vamos lembrar que a aceleração é a segunda derivada da posição. Então:
Opa! Esse é um problema que não conseguimos resolver né? Porque temos duas variáveis dependentes do tempo, x e . Mas calma, não criemos pânico! Tem duas coisas que você precisa saber que vão te ajudar a resolver isso.
Passo 3
Primeiro: para pequenas inclinações, que é o que estamos considerando, ! Então:
Segundo: nós podemos escrever x em função de . Vai ficar assim:
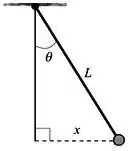
Lembrando que , então:
Vamos substituir!
Olha que maravilha, achamos a EDO do movimento do cara, só com x! Vamos comparar com a equação do MHS:
Comparando as duas teremos que . Ou seja, .
Agora só precisamos substituir no período! Temos a fórmula:
Então:
E ele tá dizendo que o período vai ser igual a !
Passo 4
Esse negócio de energia é muito chato, que Thor nos ajude! Vem comigo, foco!
Nós vamos calcular a energia cinética e a energia potencial, depois somar e provar que essa soma é constante.
Para a enérgica cinética:
Lembrando aí que a velocidade é a primeira derivada da posição:
Maravilha! Para a energia potencial:
“Valha-me Deus que coisa horrorosa, não sei calcular essa integral!” Calma, não é tão difícil quanto parece. Essa força que aparece aí é a nossa única força resultante (no eixo x, lembra que no eixo y as forças se anulam?). Então vamos trocar:
E lembrando:
Então:
Tá vendo, eu disse que não era tão difícil.
Passo 5
Agora vamos somar as energias:
Ok, agora nós precisamos achar x! Lembrando que x é solução da EDO:
E aí precisamos relembrar, lá do cálculo, que a solução dessa EDO é:
Esse é a amplitude do movimento.
Se a gente derivar isso, encontramos:
Agora vamos substituir isso tudo na fórmula da energia:
Lembrando aí que:
E substituindo:
Coisa linda de se ver! Pela identidade trigonométrica, podemos trocar esse por 1!
Como todos esses caras são constantes, a energia é constante.
Resposta
a)
b)