Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
f)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o domínio da função e esboçar o gráfico dela. Pra isso, a gente tem sempre que pensar nos valores que pode assumir na função, esse será nosso domínio.
Mas pra pensar nos valores que pode assumir, nós temos que pensar também nos valores que ele não pode assumir, ou seja, as restrições da função. Isso significa que a gente tem sempre que garantir que:
- nas frações o denominador não pode valer zero;
- dentro das raízes quadradas não pode ter número negativo;
- o valor dentro de um logaritmo tem que ser estritamente positivo.
Então, vamos verificar em qual caso cai nossa função, definir suas restrições e, assim, encontrar seu domínio.
Vamos lá!
Passo 2
Galera, nossa função é dada por:
Repare que a nossa função não cai em nenhum dos casos de restrição. Isso acontece porque, por definição, a função modular tem seu domínio definido em todo conjunto dos números reais. Então, mesmo sendo somada a uma constante, nosso domínio continua sendo:
Plotamos a nossa função módulo deslocada em unidades para cima, assim, temos :
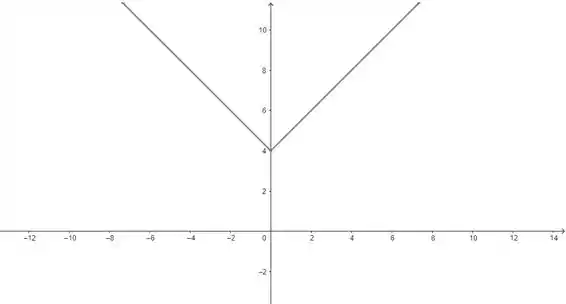
Prontinho, galera! Até a próxima! 😉