Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 5.Exercícios e Problemas - Ex. 16

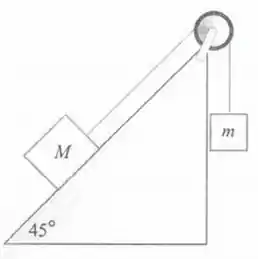
Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m .

Passo 1

Salve pessoas, tudo certo? Vamos lá! Primeiro, vamos dividir as forças de cada bloco. Para o bloco “M”, temos:

Na vertical:

N - P m ⋅ c o s 45 ° = 0

N = P m ⋅ c o s 45 °

Na horizontal:

T - F A T - P N ⋅ s e n 45 ° = M ⋅ a

Para o bloco “m”:

P m - T = m ⋅ a

Passo 2

Aqui, podemos montar um sistema de equações e soma-los! Vamos fazer com as componentes verticais e horizontais!

P m - T = m ⋅ a T - F A T - P M ⋅ s e n 45 ° = M ⋅ a

P m - F A T - P M ⋅ s e n 45 ° = a ⋅ M + m

Ignorando o atrito, ( F A T ),

P m - P m ⋅ s e n 45 ° = a ⋅ M + m

Agora temos que entender o seguinte. Para o sistema em equilíbrio, a aceleração tem que ser igualada a 0! Portanto,

P m - P m ⋅ s e n 45 ° M + m = a

P m - P m ⋅ s e n 45 ° M + m = 0

( m ⋅ g ) - ( M ⋅ g ) ⋅ s e n 45 ° M + m = 0

( m ⋅ g ) - M ⋅ g ⋅ 2 2   M + m = 0

Separando,

( m ⋅ g )   2 M + m - M ⋅ g ⋅ 2 2 ( M + m ) = 0

( m ⋅ g )   2 M + m = M ⋅ g 2 2 ( M + m )

Dividindo tudo por g:

m 2 M + m = M ⋅ 2 2 ( M + m )

Fazendo um joguinho com essas razões,

m M = M + m 2 ( M + m )

Logo,

m M = 2

m = 2 M

Passo 3

Agora calculando a aceleração dos blocos, considerando que: M = 2 m . Para isso, vamos voltar naquela equação do passo 2, que é:

P m - P m ⋅ s e n 45 ° M + m = a

( m ⋅ g ) - ( M ⋅ g ) ⋅ 2 2 M + m = a

( m ⋅ g ) - ( M ⋅ g ) ⋅ 2 2 M + m = a

Aplicando os valores de M , em relação a m ( M = 2 m ),

( m ⋅ g ) - ( 2 m ⋅ g ) ⋅ 2 2 2 m + m = a

2 m ( 2 ⋅ g   - g ) 6 m = a

Resolvendo,

a = 2 - 1 g 3

Resposta

A M = 2 m

( B ) a = 2 - 1 g 3

Resposta

A d = 948.6   m e t r o s

B θ = 121.8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um planador de 1,00k g em um trilho de ar horizontal é puxado por um fio em um ângulo θ . O fio tenso corre sobre uma polia e está ligado a um corpo de massa 0,500k g pendurado, conforme mostrado na F
Dois blocos de massa 3,50k g e 8,00k g são conectados por um fio sem massa que passa sobre uma polia sem atrito (Fig. P4.47). Os planos inclinados são sem atrito. Encontre o módulo da aceleração de ca
Na situação descrita no Problema 45 e mostrada na Figura P4.45, as massas da corda, balança de mola e polia são desprezíveis. Os pés de Nick não estão tocando o chão. Suponha que Nick esteja momentane
Na máquina de Atwood discutida no Exemplo 4.4 e mostrada na Figura Ativa 4.12a, m 1=2,00k g e m 2=7,00k g . Por comparação, as massas da polia e da corda são desprezíveis. A polia gira sem atrito e a
Uma criança inventiva chamada Nick quer pegar uma maçã em uma árvore sem escalá-la. Sentado em uma cadeira conectada a uma corda que passa sobre uma polia sem atrito (Fig. P4.45), Nick puxa a ponta so