Determine o valor da constante de equilíbrio líquido-vapor de uma mistura de 0,4 de tolueno (1) e 0,6 de isobutanol (2) a partir da equação:
Para a pressão de vapor utilize a Equação de Antoine. Para , utilize a equação de Van Laar com e .
Obs: Determine a constante de equilíbrio para os dois componentes e considere pressão igual a e temperatura de
Passo 1
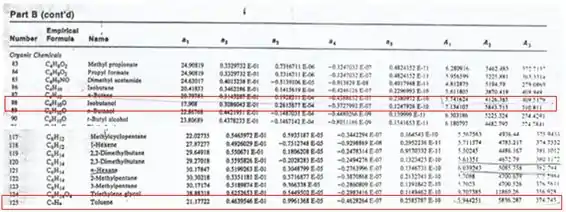
Precisamos determinar a constante de equilíbrio . Para isso, temos que determinar tanto as pressões de vapor por Antoine, quanto o pela equação de Van Laar. Para a equação de Van Laar, nós vamos utilizar:
Com e para as constante e e para as frações molares. Substituindo, temos que:
Então:
Passo 2
Para a pressão de vapor, vamos utilizar a Equação de Antoine e vamos pegar os dados nas tabelas que temos disponíves, ok?
Vamos pegar os dados de cada componente:
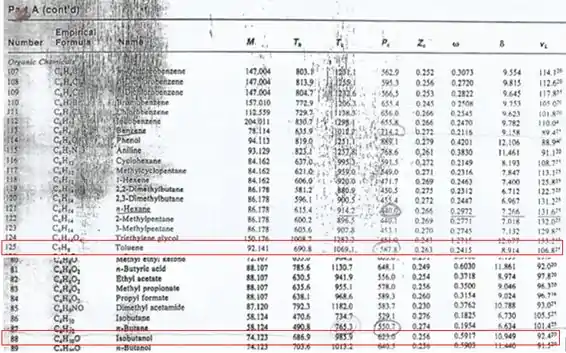
Para o tolueno, temos os seguintes dados:
Já para o isobutanol, temos os seguintes dados:
Para aplicar a Equação de Antoine, também é necessário jogar as temperaturas para Fahrenheit. Então, bora fazer essa conversão:
Então, vamos substituir a nossa temperatura de .
Passo 3
Agora, vamos substituir todos os dados nas fórmulas para encontrar a pressão de saturação de cada componente.
Para o tolueno:
Para o isobutanol:
Portanto:
Passo 4
Agora, precisamos substituir tudo que já temos na fórmula do :
Para o tolueno:
Para o isobutanol: