Os dados abaixo representam o índice de alcalinidade de certa experiência.
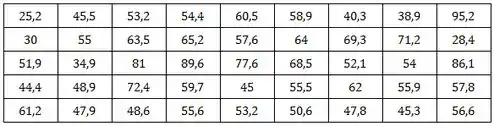
- Construa a distribuição de frequência para dados grupados (utilizando a Regra da Raiz)
- Encontre as Medidas de Posição.
- Encontre as Medidas de Dispersão.
- Construa Histograma e Polígono de frequência e analise a curva.
- Analise os resultados.
Passo 1
Como queremos dados grupados, temos que dividir os valores em classes.
O exercício pede pra usarmos a regra da raiz.
Se a gente tem 45 valores:
Vamos ter então 7 classes.
Passo 2
O maior valor que temos é 95,2 e o menor é 25,2.
A amplitude total da amostra é então:
Com isso, cada classe vai ter uma amplitude igual a:
Ou seja vamos ter classes de 10 em 10:
Passo 3
(a)
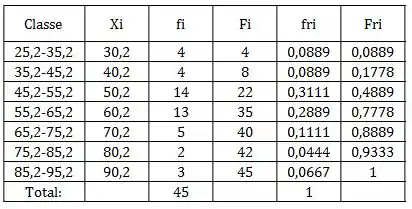
pra construir a distribuição de frequência vamos montar uma tabela com:
Que é quantos valores existem dentro de cada classe;
Só ir somando as anteriores;
Que é dividir pelo total de valores que no caso são 45;
Que é dividir pelo total de valores (45).
Passo 4
Ficaria algo assim:
Passo 5
(b)
Medidas de posição são: média, moda e mediana.
Para dados grupados calculamos a média usando:
Passo 6
Para calcular a moda, temos primeiro que achar a classe modal que é a classe com a maior frequência absoluta.
No casso é a classe que tem .
Aí usamos a fórmula:
Passo 7
Pra calcular a mediana, temos primeiro que identificar a classe da mediana.
Para isso calculamos o valor de que será .
Agora, olhando para os valores de procuramos em qual classe estará o valor 22,5. Percebemos que a classe tem . Como queremos 22,5 não usaremos essa e sim a seguinte.
No nosso caso a classe da mediana será .
Ai usamos a fórmula:
Passo 8
(c)
Medidas de dispersão são: variância, desvio padrão e coeficiente de variação.
Para a variância vamos usar a fórmula:
Desvio padrão:
Coef. De variação:
Passo 9
(d)
Construindo o nosso histograma e o polígono de frequência:
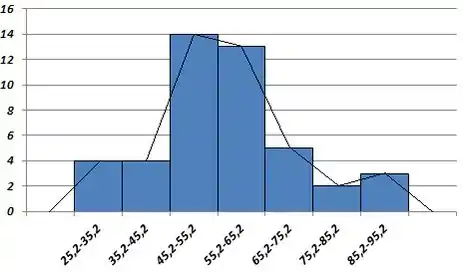
A curva é assimétrica, pois
Passo 10
(e)
Temos que dizer se a curva é homogênea ou não.
Como o valor do é pequeno, a distribuição é dita homogênea.
Resposta
Ei, a resposta está no passo a passo :)