P1 de Física 3 - FIS1051 da PUCRIO - 2013.2

Uma linha uniforme de cargas de comprimento e a carga total produz um campo elétrico a uma distância da linha ao longo da sua mediatriz que é dado pela equação: .

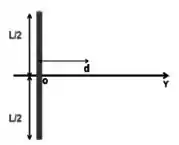
Considere agora um sistema constituído por uma calha cilíndrica isolante de comprimento , raio de curvatura , carregada uniformemente com carga total positiva. A origem dos eixos está situada sobre o eixo da calha, a uma distância da superfície lateral da mesma, e no plano mediano que corta a calha em duas partes idênticas de comprimento . A interseção da calha com o plano descreve um arco de circunferência de ângulo igual a , com , como representado na figura.

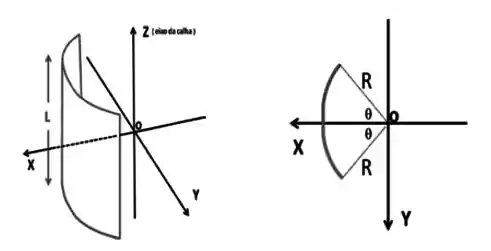
Considere a calha como constituída por fios de carga infinitesimal , largura e comprimento . Calcule a carga infinitesimal de cada fio. (A densidade superficial de carga da calha é )

Considerando que , obtenha o módulo, direção e sentido do campo elétrico gerado pela calha carregada na origem dos eixos .

Um plano infinito carregado uniformemente é agora colocado paralelamente ao plano cortando o eixo na coordenada . Nesta condição, nota-se que o campo elétrico resultante na origem é nulo.

Calcule a densidade superficial de carga do plano infinito carregado.

Uma seção de comprimento do cilindro infinito de raio , mostrado na Figura 1, tem carga total . Esta carga se distribui no volume definido pela seção de acordo com densidade volumétrica de carga . A densidade não varia ao longo do eixo do cilindro, o que permite definir a densidade linear de carga . Determine a relação entre e , considerando os valores de e conhecidos.

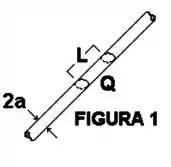
Determine o módulo do vetor campo elétrico em um ponto qualquer afastado da distância (onde do eixo do cilindro infinito (Figura 1), considerando o valor de conhecido.

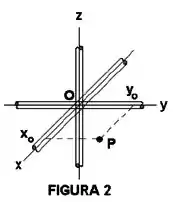
Três cilindros idênticos (raio e densidade linear de carga ) estão alinhados com os eixos coordenados, conforme mostra a Figura 2. Determine o vetor campo elétrico em um ponto de coordenadas situado no plano e fora dos três cilindros, desprezando as distorções devidas à junção situada em torno da origem.

A figura ilustra uma coroa circular disposta no plano , centrada na origem, de raio interno e raio externo . Sua carga está uniformemente distribuída e possui . Use ou .

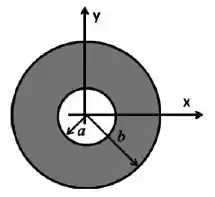
Considerando a referência para potenciais no infinito, encontre o valor do potencial elétrico num ponto qualquer do eixo , à distância da origem.

Calcule o potencial no ponto e o valor do trabalho realizado pela força eletrostática no deslocamento de uma carga teste desde até o ponto onde o potencial vale .

Suponha que o potencial gerado pela coroa circular no ponto tenha valor . Queremos anular o potencial em , e para isso dispomos de uma carga pontual de valor . Determine todos os pontos do espaço em que podemos posicionar a carga de modo a tornar nulo o potencial em .