P1 de Física 3 - FIS1051 da PUCRIO - 2014.1

Um fio de comprimento está carregado uniformemente com a densidade linear de carga . Determine uma expressão para o potencial elétrico em um ponto arbitrário do eixo , conforme mostra a Figura .

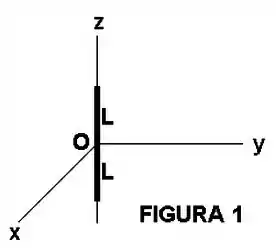
Adapte a solução do item para determinar o potencial elétrico devido a um fio quadrado de lado , carregado uniformemente com a densidade linear de carga , em um ponto de observação arbitrário do eixo , conforme mostra a Figura .

Sugestão: calcule a distância entre o ponto de observação e o ponto médio de um dos lados do quadrado.

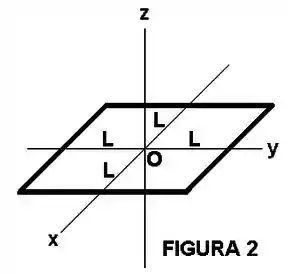
Determine o vetor campo elétrico devido ao fio quadrado no mesmo ponto de observação.

Uma partícula com carga foi depositada bem no centro da cavidade de uma casca esférica condutora de raio interno e raio externo . O gráfico ao lado da figura mostra o fluxo através de uma esfera gaussiana com centro na partícula em função do raio da esfera.

(Considere ou .)

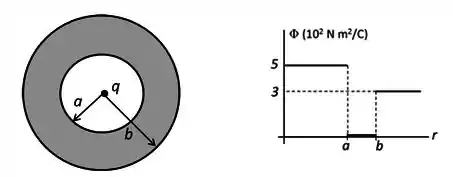
Determine a carga da partícula central e a carga líquida presente na casca condutora.

Considere agora que e . Encontre a dependência do campo elétrico como função de , para as três regiões: , e . Depois , copie na folha de respostas o par de eixos a seguir e esboce nele a função encontrada, calculando os valores importantes e explicitando no gráfico.

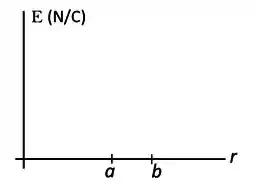
Remove-se a partícula e a cavidade é preenchida com um material isolante. A carga no isolante apresenta simetria esférica e densidade volumétrica dada pela função , onde é uma constante. Esta distribuição de carga provoca um campo elétrico radial e de módulo constante e igual a dentro da cavidade. Calcule o valor da constante com sua respectiva unidade SI.

Considere os dois semicírculos concêntricos de material isolante representados na figura abaixo. O semicírculo com raio tem densidade linear de carga positiva , enquanto o semicírculo menor tem raio e duas densidades lineares de carga: (positiva) para pontos com coordenada negativa e (negativa) para pontos com coordenada positiva. Os raios e as densidades lineares das duas distribuições de carga são tais que vale a relação .

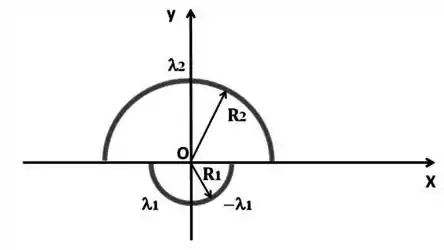
Calcule o vetor campo elétrico gerado pelo semicírculo menor no ponto (origem dos eixos e centro dos semicírculos)

Calcule o vetor campo elétrico gerado pelo semicírculo maior no ponto .

Calcule o vetor de campo elétrico resultante do ponto e escreva seu módulo.

Calcule as coordenadas da posição na qual deve ser colocada uma carga puntiforme negativa de valor , para que o campo elétrico total resultante no ponto seja nulo.