P1 de Física 3 - FIS1051 da PUCRIO - 2016.1
Física 3 - FIS1051 - PUCRIO
O anel de raio mostrado na Figura contém uma carga total uniformemente distribuída. O potencial elétrico devido ao anel em um ponto qualquer do eixo é:
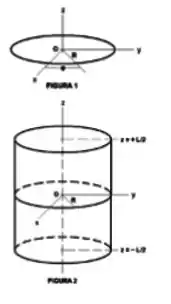
(a) Use o resultado acima para determinar uma expressão para o potencial elétrico em um ponto arbitrário do eixo devido a um disco de raio carregado com a densidade superficial , onde é a distância de um ponto do disco ao seu centro (Figura ).
Suponha agora que a casca cilíndrica da Figura seja longa e que os pontos de interesse sejam externos a ela e próximos da sua superfície, mas afastados de suas extremidades.
(b) Determine o vetor campo elétrico em um ponto de interesse arbitrário, em função da distância ao eixo da casca cilíndrica.
(c) Use o resultado do item anterior para determinar a diferença entre os potenciais elétricos (ddps) de pontos de interesse situados em e .
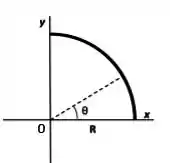
Ver solução completaO arco de um quarto de circunferência de raio , mostrado na figura abaixo, possui uma distribuição de carga não uniforme dada por , sendo uma constante positiva.
(a) Calcule a carga total presente no arco, em função de e de .
(b) Calcule (em função de , de e da constante de Coulomb ) as componentes e com os respectivos sinais, do vetor campo elétrico criado pelo arco sobre o ponto localizado na origem.
Considere agora que o arco gere, em um ponto qualquer, um campo elétrico e que neste mesmo ponto seja colocada uma carga puntiforme .
(c) Encontre o vetor da força elétrica exercida pelo arco sobre a carga.
Duas cascas esféricas condutoras concêntricas e , têm a disposição indicada na figura abaixo. A casca tem raio interno , raio externo e está carregada com uma carga líquida . A casca tem raio interno , raio externo e está carregada com uma carga líquida desconhecida .
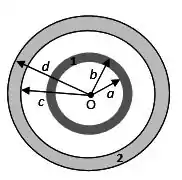
Medidas realizadas no sistema mostram que:
- o fluxo elétrico através de uma superfície gaussiana esférica de raio é igual a
- a densidade de carga na superfície externa da casca é igual a .
Com estas informações responda aos itens abaixo:
(a) Qual é o valor da carga líquida na casca ?
(b) Encontre o campo elétrico nas regiões e .
(c) Desenhe as cascas concêntricas e calcule (indicando também no desenho) as distribuições de carga nas superfícies internas e externas das duas cascas esféricas.
(d) Considere agora que no centro do sistema das cascas (ponto ) seja colocada uma carga puntiforme negativa de valor . Calcule o novo valor da densidade de carga na superfície externa da casca .
Ver solução completa