P1 de Física 3 - FIS1051 da PUCRIO - 2018.1

Seja um fio isolante fino (que pode ser considerado reto e infinito) carregado com uma densidade linear de carga uniforme . Este fio está colocado paralelamente e concentricamente com um cilindro condutor (também infinito), de raio interno e raio externo , como mostra a figura 1 abaixo. O cilindro condutor possui, inicialmente, uma densidade linear de carga uniforme .

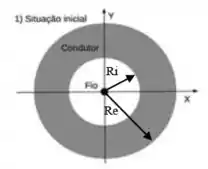
1. Calcule as densidades superficiais de carga e , respectivamente, nas superfícies interna e externa do cilindro, considerando que o equilíbrio eletrostático foi atingido.
2. Calcule o campo elétrico nas regiões , e .

Agora suponha o cilindro anterior seja substituído por um cilindro isolante, com dimensões idênticas e com exatamente a mesma distribuição de cargas que nos itens a) e b). O mesmo fio usado anteriormente é, então, deslocado ao longo do eixo , de modo que seu centro se encontra agora em , como mostrado na figura 2 abaixo.

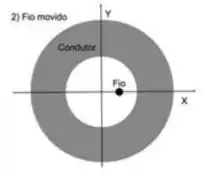
c) Calcule o campo elétrico no ponto .

Considere a coroa circular da figura 1, raio interno e raio externo , com densidade superficial de carga não uniforme dada pela função , onde é uma constante positiva e é a distância a partir do centro. Considere também o ponto no eixo da coroa, à altura do centro. A figura 2 mostra um anel de raio e carga total . Sabe-se que o potencial geral em pelo anel é dado por

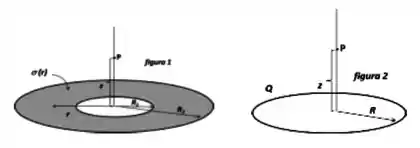
a) Adaptando o resultado do potencial do anel, utilize a relação para encontrar o potencial gerado pela coroa circular em .

Suponha, agora, que uma carga pontual , inicialmente em repouso no ponto , é solta e cruze a origem , submetida à força elétrica (desconsidere, portanto, a força de gravidade).

b) Para que isso aconteça, que sinal deve ter a carga e qual será a sua energia cinética final ao cruzar a origem?

Desconsidere, agora, a carga e suponha que o potencial geral pela coroa circular em tenha o seguinte valor: . Imagine uma casca esférica isolante de espessura infinitesimal seja colocada envolvendo toda a coroa circular e também o ponto . A casca esférica possui uma carga uniformemente distribuída em sua superfície.

c) Calcule que raio a casca esférica deve ter para que o potencial total em seja nulo. (Considere ).

Duas cargas puntiformes, cada uma com carga positiva , estão fixadas a uma distância entre elas. Considere uma terceira carga , também positiva, posicionada em uma altura genérica ao longo da bissetriz do eixo que separa as cargas (veja a figura abaixo) e inicialmente em repouso. A carga só pode se mover ao longo desta bissetriz.

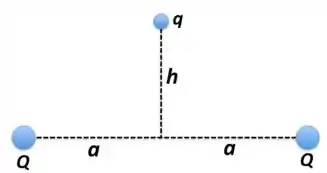
Escolha um sistema de coordenadas apropriado. Em seguida:

1. Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas cargas iguais a sobre a carga .
2. Encontre a distância para a qual o módulo da força exercida sobre a carga é máximo.
3. Calcule o módulo, direção e sentido da força elétrica no item b).

Considere, agora, que a carga da esquerda seja trocada por outra com o sinal negativo, .

d) Calcule, nesta nova condição, as respostas dos itens b) e c).