P2 de Física 3 - FIS1051 da PUCRIO - 2018.1
Física 3 - FIS1051 - PUCRIO
Caso 1
O gráfico mostra o comportamento do módulo do campo magnético criado por um fio retilíneo cilíndrico muito longo como função da distância radial até seu eixo de simetria. Para , é linear. Para , a função é inversamente proporcional a .
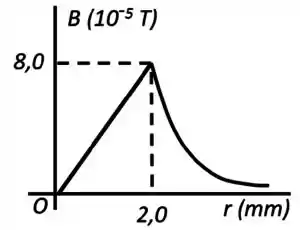
- A densidade de corrente é uniforme dentro do fio? Justifique a sua resposta cuidadosamente usando a lei de Ampère.
- Suponha, agora, que a corrente no fio sentido e que a densidade de corrente seja uniforme. Calcule o vetor , em .
- Em função de e , calcule a razão de modo que a força magnética resultante do fio sobre a espira seja nula.
Caso 2
Considere, agora, uma espira em forma de trapézio (figura abaixo), que tem dois lados paralelos entre si e também paralelos a um fio muito longo pelo qual passa uma corrente .
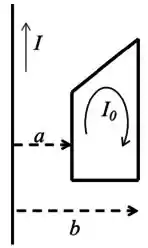
Pela espira circula uma corrente no sentido horário, mas seus lados não paralelos estão blindados do campo magnético causado pelo fio. O segmento da espira mais próximo ao fio e está à distância do fio, e o segmento mais distante mede e está à distância do fio.
a) Um condutor reto infinito conduzindo uma corrente é dividido em duas partes semicirculares idênticas de raio . Cada parte semicircular conduz a corrente , conforme mostra a Figura 1. Calcule o vetor campo magnético no centro da espira circular assim formada.
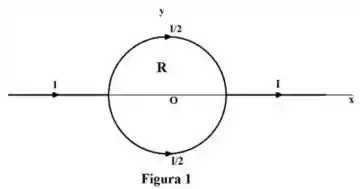
b) Um condutor reto infinito conduzido uma corrente é dobrado conforme mostra a Figura 2. Os fios paralelos semi-infinitos são muito próximos, de modo que suas correntes (opostas) se cancelam mutuamente. Calcule o vetor campo magnético no centro da espira circular assim formada.
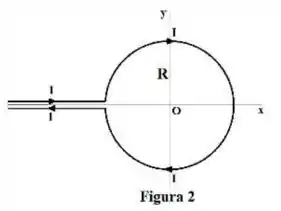
c) Calcule o vetor campo magnético devido aos fios semi-infinitos da Figura 1 (que conduzem a corrente ) em um ponto arbitrário do eixo vertical (perpendiculares ao papel) que contém o centro da espira circular. Sugestão: os dois fios semi-infinitos que conduzem a corrente são equivalentes a um fio infinito que conduz a corrente e um fio finito que conduz a corrente .
Ver solução completaConsidere o circuito RC da figura, onde , , é um capacitor de placas paralelas de área , com separação de , tendo um meio entre as placas de constante dielétrica , e . e são duas chaves.
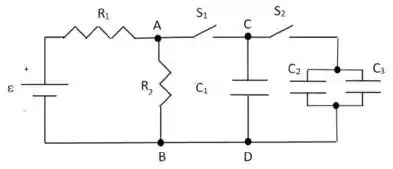
Todos os capacitores estão inicialmente descarregados. Neste circuito, ocorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberto durante longo tempo.
Fase 2: chaves e abertas e o dielétrico substituído por outro de .
Fase 3: chave aberta e fechada.
Fase 4: chaves e fechadas.
Determine:
- A capacitância .
- As correntes em e no instante inicial da fase 1.
- A energia armazenada em e a potência dissipada em no final da fase 1.
- O trabalho externo necessário para substituir o meio dielétrico na fase 2.
- A diferença de potencial no final das fases 1, 2 e 3.
- A corrente em (sentido e intensidade) no início da fase 4.
Em todos os cálculos, considere .
Ver solução completa