P2 de Física 3 - FIS1051 da PUCRIO - 2019.2

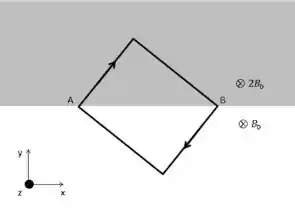
Uma espira retangular de lados e é colocada em duas regiões: a superior com campo magnético e a inferior com como mostra a figura ao lado. A espira é percorrida por uma corrente de intensidade no sentido apresentado na figura.

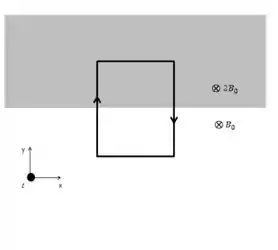
a) Qual deve ser a massa da espira (preste atenção no sentido da gravidade na figura) para que ela fique suspensa no ar?

b) Qual deve ser o novo valor da massa para que a espira permaneça em equilíbrio quando mudamos sua orientação para a mostrada na figura inferior?

Um cilindro condutor muito comprido, com o seu eixo orientado ao longo do eixo , transporta uma corrente elétrica cuja densidade é . A densidade de corrente, definida como a corrente por unidade de área, é simétrica em relação ao eixo do cilindro, mas não é uniforme e varia radialmente de acordo com a seguinte relação:

Onde “” é o raio do cilindro, “” é a distância radial entre o ponto considerado e o eixo do cilindro e “” é uma constante com unidades [].

a) Calcule o valor da corrente total que passa através da seção reta do fio.

b) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região.

c) Obtenha a expressão para a corrente contida em uma seção reta circular de raio , centralizada no eixo do cilindro.

d) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região .

e) Como se comparam os resultados dos itens b) e d) quando ?

Considere o circuito ao lado, onde os valores de , , , e são conhecidos e os capacitores , e encontram-se inicialmente descarregados. Em seguida, os capacitores e são carregados fechando-se a chave e mantendo-se a chave aberta.

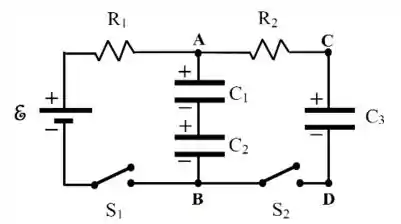
a) Apresente uma expressão para tensão (ddp) no resistor em função do tempo, a partir do instante em que a chave é fechada.

b) Calcule também a energia total armazenada nos dois capacitores e , supondo que a chave permaneceu fechada durante muito tempo.

Agora considere que seja aberta, depois de ter permanecido fechada durante muito tempo. Sabe-se que, neste instante, . Simultaneamente, os capacitores e são conectados ao capacitor descarregado fechando-se a chave que assim permanece durante muito tempo.

c) Calcule as tensões (ddps) finais entre os terminais dos capacitores e .

d) Calcule a energia total armazenada nos capacitores e ao final do processo. Compare com a energia armazenada nos capacitores e imediatamente antes do fechamento da chave . Por que elas são diferentes?