P3 de Física 3 - FIS1051 da PUCRIO - 2020.1
Física 3 - FIS1051 - PUCRIO
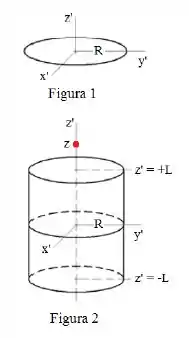
O anel de raio mostrado na Figura 1 contém uma carga total uniformemente distribuída.
a) Determine uma expressão para o potencial elétrico devido ao anel em um ponto qualquer do eixo ;
b) Determine o potencial elétrico devido à casca cilíndrica de e carregada com uma densidade superficial de carga uniforme, mostrada na Figura 2, no ponto do mesmo eixo;
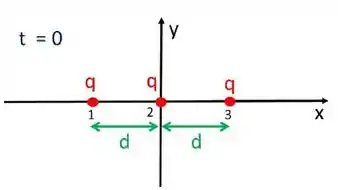
Três partículas idênticas, de massa e carga, se encontram no instante nas posições iniciais , ao longo do eixo , como mostra a Figura. Não considere nenhuma outra força, além das forças eletrostáticas, agindo sobre as partículas.
a) Calcule as forças resultantes sobre cada uma das partículas e, no instante inicial.
b) Calcule a energia eletrostática total no instante inicial.
Após o instante , as partículas são liberadas do repouso para se moverem livremente sob a ação das forças eletrostáticas.
c) Após um tempo muito longo, calcule as posições e velocidades de cada uma das três partículas acima.
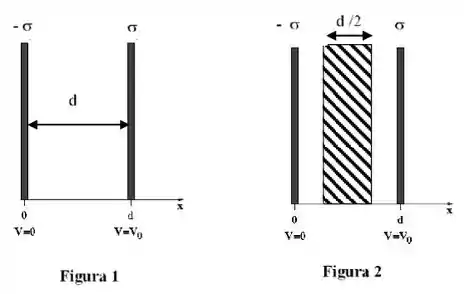
Duas placas isolantes muito grandes e de espessura desprezível são colocadas paralelamente uma em relação a outra, como mostrado na Figura 1. Na placa à direita, há uma distribuição superficial uniforme de cargas positiva. Na placa à esquerda, a distribuição de cargas é também uniforme, porém de densidade superficial igual e oposta à da direita. A distância entre as placas vale d e existe o vácuo entre as duas. Tomando a placa à esquerda (na posição ) como o referencial para o potencial mede-se que, sobre a placa à direita , o potencial tem valor.
a) Calcule a densidade superficial de cargas, , da placa isolante positiva em função de .
b) O sinal de é positivo ou negativo? Justifique.
Suponha agora que uma placa condutora neutra de espessura seja colocada na região entre as duas placas isolantes, como mostrado na Figura 2. Nesta nova configuração:
c) Calcule os valores do potencial em e faça um gráfico do potencial em função da distância para .
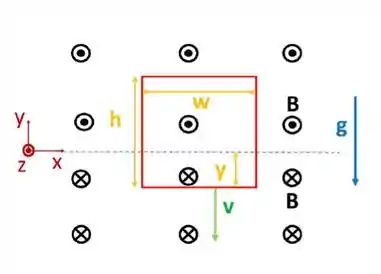
Um arame metálico forma um circuito retangular, de altura , largura e massa. Esse arame tem uma resistência total igual a . Na Figura, podemos ver que, em um certo instante de tempo, uma parte do aro está e outra em . O plano (linha azul tracejada) separa a região onde o campo magnético aponta na direção da região onde o campo magnético aponta na direção , como mostra a Figura. Observe a distância entre a linha tracejada azul e o braço horizontal inferior da espira.
Se , temos ; Se , .
Suponha que esse aro cai com velocidade vertical v constante sob a ação apenas de seu próprio peso e das forças magnéticas agindo sobre ele. Todas as respostas abaixo devem ser apresentadas apenas em função das variáveis do problema: (use apenas as necessárias).
Quando o aro está colocado como mostra a Figura, para todos os itens:
- Calcule a taxa de variação no tempo do fluxo magnético sobre o aro
- Calcule a sobre o aro e a corrente induzida. Seu sentido é horário ou anti horário? Justifique sua resposta
- Calcule a força magnética resultante sobre o aro
- Calcule o valor da velocidade constante com que o aro cai. Lembre-se que a velocidade é um vetor
- Calcule o valor da potencia elétrica dissipada no aro
- Calcule a potencia fornecida elo trabalho da força peso sobre o aro. Calcule
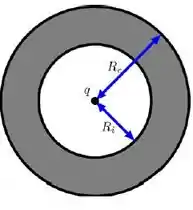
Considere uma carga pontual q posicionada no centro de uma casca esférica isolante de raio interno e raio externo. A casca possui uma carga total distribuída homogeneamente em seu volume.
A Figura serve como guia.
a) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal).
Ou seja,
b) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal). Ou seja, .
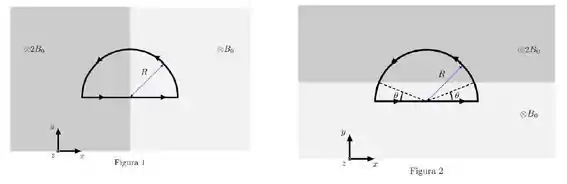
Uma espira semicircular de raio está posicionada entre duas regiões de campo magnético constante (nas Figuras 1 e 2, a região cinza-claro) e (nas Figuras 1 e 2, a região cinza-escuro). A espira é percorrida por uma correnteno sentido indicado nas Figuras 1 e 2. Observe que, na Figura 1, as metades da espira se encontram em regiões distintas. Calcule o vetor força magnética resultante na espira devido aos campos magnéticos de cada região, quando a espira se encontra:
- Posicionada como mostra a figura ;
- Posicionada como mostra a figura , onde o ângulo é .
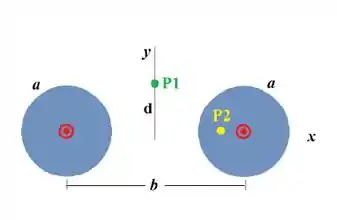
Os dois fios retos, infinitos e paralelos ao eixo z têm raios a. Seus eixos, contidos no plano e também paralelos ao eixo, estão afastados conforme mostra a Figura. São percorridos por correntes iguais, uniformemente distribuídas nos seus interiores com densidade no sentido Determine o vetor campo magnético nos pontos:
- de coordenada .
- de coordenada .
- O vetor força (por unidade de comprimento) exercida pelo fio da esquerda sobre o fio da direita, de .
Em seguida, suponha que as correntes totais estejam concentradas nos respectivos eixos e determine:
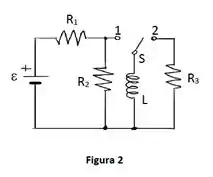
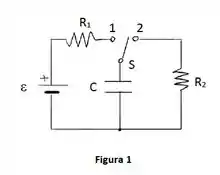
Considere o circuito da Figura 1, onde e S é uma chave que alterna entre as posições 1 e 2 de forma cíclica, de tal forma que a permanência em cada posição tem a duração de 1 segundo.
- Desenhe o gráfico em escala da variação da . no capacitor com dois ciclos da chave S, indicando nos eixos os valores numéricos importantes. NOTA: considere .
- Determine para que a em no inicio da fase seja igual a .
- Com o valor de calcule a corrente fornecida pela bateria no inicio da fase .
-
1 e o indutor na figura fossem plenamente energizados nos respectivos circuitos e depois conectados diretamente entre si, formando um circuito , qual seria a frequência angular de oscilação e a amplitude da voltagem do capacitor, após o sistema entrar em oscilação estável?
Considere agora o circuito da Figura 2, onde , o indutor está inicialmente sem energia e ocorrem as seguintes fases sucessivas:
- Fase 1: chave S na posição 1 durante longo tempo;
- Fase 2: chave S na posição 2 durante longo tempo.