2CH de Física 3 da UFRJ - 2019.2

. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.

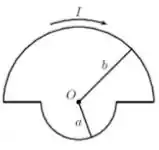
Determine o vetor momento de dipolo magnético da espira.

. Considere uma barra fina, retilínea e isolante, de comprimento , disposta sobre o eixo de um sistema de coordenadas com uma de suas extremidades sobre a origem, como mostra a figura abaixo. Ela encontra-se carregada com uma densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva.

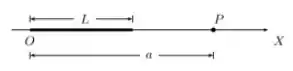
Determine a carga total da barra.

Determine o vetor campo elétrico em um ponto sobre o eixo , localizado a uma distância da extremidade da barra que está sobre a origem .

. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.

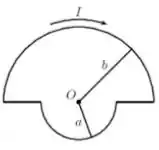
Deduza, em detalhe, uma expressão para o vetor campo magnético produzido pela espira

no ponto , que corresponde ao centro comum dos trechos semicirculares.

. Um plano infinito é posicionado sobre o plano de um sistema de coordenadas. Ele encontra-se carregado com uma densidade superficial de carga constante .

Sabendo que o campo elétrico produzido pelo plano em um ponto qualquer do espaço tem a forma , utilize a lei de Gauss para determinar , considerando as regiões e .

Determine o potencial elétrico produzido pelo plano no ponto , considerando as mesmas regiões acima. Considere que o potencial é nulo sobre o próprio plano.

. Uma barra condutora fina se move com velocidade constante sobre um par de trilhos condutores finos, como mostrado na figura abaixo. O trecho em que os trilhos estão angulados tem um comprimento horizontal e a separação entre os trilhos no trecho em que eles são paralelos vale . No instante , a barra se encontra no ponto onde os trilhos se encontram. O atrito entre os trilhos e a barra é desprezível e todo o sistema está imerso em uma região de campo magnético constante .

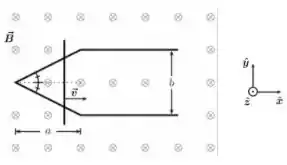
Determine o módulo do fluxo de campo magnético através da área definida pelos trilhos e a barra como função do tempo , considerando os intervalos e . Sugestão: Para o intervalo , utilize uma semelhança de triângulos para obter uma relação entre a porção de comprimento da barra dentro do circuito e o seu deslocamento horizontal.

Determine o módulo e o sentido da força eletromotriz induzida no sistema como função do tempo , considerando os mesmos intervalos.

(c) Esboce os gráficos dos módulos do fluxo e da força eletromotriz induzida como função de , destacando os valores relevantes.