PSub de Física 4 da USP - 2018

Uma estrela de raio irradia a uma temperatura absoluta . Tratando a estrela como um corpo negro, determine a fórmula para a massa perdida pela estrela num intervalo de tempo .

Considere o átomo de hidrogênio composto por um elétron que transita do estado para o estado , emitindo um fóton.

Encontre o comprimento de onda do fóton emitido, em .

Dado que a transição acima ocorre num intervalo de tempo de , encontre a incerteza de , em .

Considere uma estrela situada à uma distância medida por um observador em repouso na Terra. Um astronauta parte da Terra em direção à estrela com velocidade .

Sob o ponto de vista do astronauta, qual é a distância percorrida e o tempo de viagem até a estrela?

Qual é a duração da viagem Terra-estrela medida pelo observador na Terra?

Se na metade da viagem (para o observador na Terra) o astronauta emitir um sinal de luz em direção à Terra, quanto tempo depois da partida do astronauta esse sinal será observado pelo observador na Terra?

Uma película muito fina de material transparente, de índice de refração é utilizada como revestimento antirrefletor na superfície de um vidro de índice de refração de uma célula solar. Qual deve ser a espessura mínima da película para uma incidência perpendicular não ser observar por reflexão da luz que no vácuo tem comprimento de onda ?

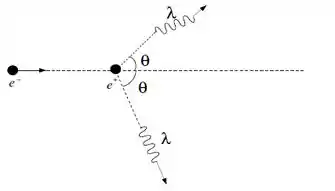
Um elétron, com massa de repouso e energia cinética colide com um pósitron em repouso produzindo dois fótons, conforme ilustrado na figura abaixo. O pósitron é uma partícula com a mesma massa de repouso do elétron, porém com carga oposta.

Determine o comprimento de onda dos fótons em função de e .

Encontre o ângulo de espalhamento.

As funções de onda correspondentes aos estados estacionários de uma partícula de massa que se move em uma dimensão confinada em um poço de potencial infinito de largura são dadas por

Determine a expressão para o comprimento de onda de de Broglie desta partícula para o estado correspondente a

Estime a incerteza mínima na medida do momento linear desta partícula no estado .

Suponha agora que no instante , a partícula encontra-se em um estado dado pela superposição de dois estados estacionários na forma , onde e representam a parte espacial das soluções estacionárias para e , respectivamente, e uma constante. Obtenha e . Expresse sua resposta em termos de e e das demais grandezas que caracterizam o sistema.

O estado acima é um estado estacionário? Justifique sua resposta.