Mostre matematicamente que é possível explorar a velocidade terminal para separar partículas de iguais tamanho e morfologia imersas em um mesmo fluido e que diferem apenas no material.
Suponha constante.
Passo 1
Basicamente, essa questão está perguntando se partículas de iguais tamanho e morfologia imersas em um mesmo fluido e que diferem apenas no material têm velocidades terminais diferentes.
O que vou fazer é chamar uma partícula de 1 e outra de 2 e escrever as velocidades terminais delas, de forma genérica:
Repara que eu chamei a densidade da 1 de e a da 2 de . Vou considerar que 1 é a mais densa, ou seja, .
Agora, vamos comparar essas duas velocidades. Vou escrever uma do lado da outra e, como ainda não sei se essas velocidades são , vou colocar uma interrogação entre elas. O objetivo do problema vai ser determinar qual sinal matemático a interrogação é.
Passo 2
Vamos buscar formas de simplificar o problema, ver o que é constante, jogar pra fora da raiz e sair cortando coisas dos dois lados.
Primeiro de tudo, tanto a área projetada como o volume podem ser escritos como uma constante (que depende da morfologia da partícula) vezes uma potência do diâmetro. Para o volume, essa constante é o fator de forma ; para a área projetada, não tem nenhuma constante específica, então bora dizer que essa constante é .
Agora começamos a cortar as coisas haha:
- Se as partículas têm a mesma morfologia: e
- Se as partículas têm o mesmo tamanho:
- Estando as partículas no mesmo fluido, estamos com iguais
- Nada foi falado sobre diferentes campos de força em cada caso, daí é um só
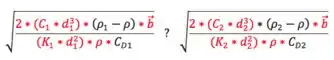
Cortei tudo que era igual, mas repara que não podia cortar esse do numerador porque ele tá dentro de um parêntesis então não tenho como tirar ele da raiz pra cortar. O enunciado diz para assumir constante, daí:
Como e é igual:
Daí:
Ou seja, provamos que quanto mais densa (maior ) a partícula, maior a velocidade terminal dela.
Passo 3
“Mas, Marcelo, o enunciado diz que é pra ser assumido constante...por que você não cortou logo ele junto com os outros?” Só porque quero comentar um pouco mais sobre eles com você haha. O que a questão pediu já acabou lá no passo 2.
Vimos lá na teoria que depende de e , isto é, . Como a morfologia é igual nos dois casos, sobra apenas pra analisar. A fórmula do é
Escrevendo pras duas partículas:
Já vimos que e os diâmetros são iguais:
Assumindo constante, vimos que , daí:
Um spoiler do próximo capítulo é que conforme aumenta, ou diminui ou fica constante; nunca aumenta. Ou seja, quem tiver velocidade terminal maior teria menor , já que estamos avaliando todos outros termos do iguais e iguais. Daí, voltando pra:
Como , e os estão no denominador, o lado esquerdo poderia ficar maior ainda.
E pra que eu falei isso tudo do ? Pra você NÃO pensar que ficaria tipo um cabo de guerra entre e . O que acontece, na verdade, é que eles vão por mesmo lado: se aumenta, diminuir, contribuindo pra aumentar.
Resposta
Ei, a resposta está no passo a passo :)