Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
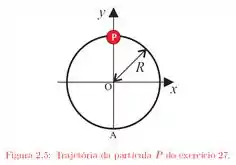
(d) A velocidade instantânea e a aceleração instantânea para e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a velocidade e a aceleração instantâneas, nos instantes e . A velocidade é tangencial à trajetória circular e pode ser calculada através da equação:
Onde é o raio da circunferência, que nós sabemos que é de , e é o período, que nós sabemos também que é de .
Já a aceleração, vai ser calculada ao longo da direção radial, no sentido do centro da trajetória circular, sendo dada pela fórmula:
Então, a direção da aceleração também vai depender do vetor posição no instante dado.
Vamos lá!
Passo 2
Como a gente já viu como calcula a velocidade, vamos substituir os dados na fórmula:
Calculando e simplificando:
E para a aceleração, usando o resultado de , vamos ter:
Passo 3
Nos intantes dados a velocidade e aceleração tangenciais não se alteram, porque se trata de um movimento circular uniforme, o que vai mudar é apenas a direção do vetor. Como a gente viu no item (a), o vetor posição em é dado por e para , temos . Assim, já que a velocidade é sempre tangente à trajetória e o vetor aceleração aponta no sentido do centro da circunferência, podemos escrever nossos resultados na forma vetorial assim:
E aceleração:
Valeu, galera! Até a próxima! 😉
Resposta
e
e