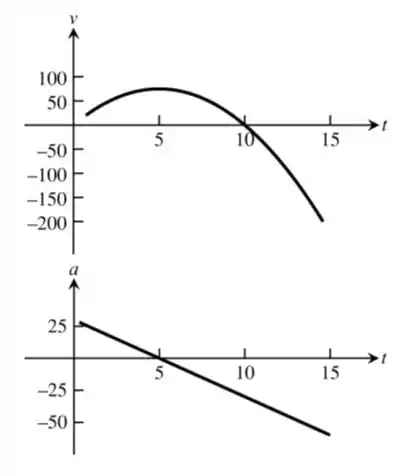
20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em e retorna 15 h mais tarde, em t = 15.
a. Use a técnica descrita no Exemplo 3 da Seção 3.2 para fazer o gráfico da velocidade do caminhão v = ds/dt para 0
b. Suponha que . Faça o gráfico de ds/dt e de ,
comparando-o com aquele no item (a).
Passo 1
a.
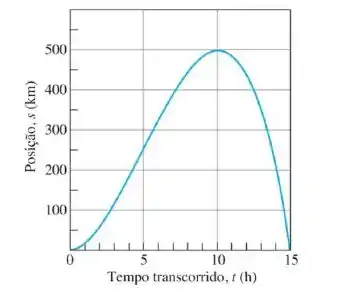
Devemos esboçar as tangentes em intervalos frequentes no gráfico e com seus coeficientes angulares estimamos os valores de nesses pontos, pois .
Então a gente registra os pares em um gráfico e unimos esses pontos com uma curva suave.
Devemos obter um gráfico parecido com esse:
Passo 2
a.
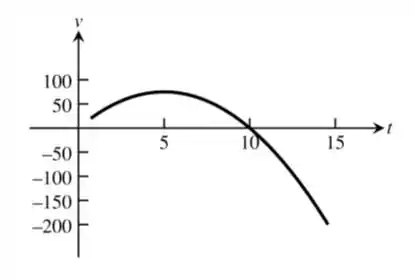
Agora devemos fazer a mesma coisa com esse gráfico, para acharmos o gráfico da aceleração em função do tempo.
Devemos obter um gráfico parecido com esse:
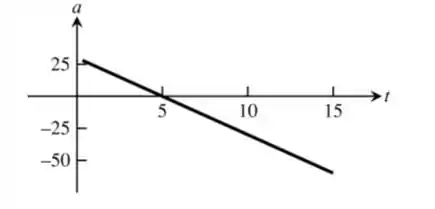
Resposta