Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 50
50-A figura abaixo mostra o gráfico de . Use o método do Exemplo 5 para aproximar as raízes da equação com uma precisão de duas casas decimais.
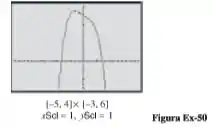
Passo 1
Bom, o que nós temos que fazer é encontrar um intervalo um intervalo de comprimento que contenha uma das raízes, então o ponto médio desse intervalo aproximará a raiz com um erro de, no máximo, (com uma precisão de duas casas decimais, que é o que o exercício pede, sacou ???).
Galera, para acharmos o intervalo que contém uma das raízes nós devemos usar o Teorema do Valor Intermediário, que nos diz o seguinte:
Se for uma função contínua em e se e forem diferentes de zero com sinais opostos, então existe, no mínimo, uma solução para a equação no intervalo .
Agora que está tudo esclarecido, vamos começar a questão!! ;)
Passo 2
Primeiro, nós temos que encontrar um intervalo de comprimento e, em seguida acharemos um outro intervalo de .
Cara, nós temos que:
e
Isso quer dizer que nesse intervalo , nós temos a nossa raiz. No entanto, nós precisamos de um intervalo de comprimento , para alcançarmos isso, vamos ter que testar alguns valores (sim, vai ser chato mesmo):
Bom, temos um novo intervalo com comprimento de 0,1, que é esse aqui:
Testando outros valores para acharmos um intervalo de comprimento , temos:
Agora sim, temos um novo intervalo de comprimento :
Como nós já havíamos discutido antes, o ponto médio desse intervalo será a raiz que nós procuramos, com um erro de no máximo, . Assim,
Infelizmente, a questão não acaba por aqui porque ainda temos que encontrar a outra raiz, mas vai ser rápido, eu juro.
Passo 3
Primeiro, nós temos que encontrar um intervalo de comprimento e, em seguida acharemos um outro intervalo de .
Cara, nós temos que:
e
Isso quer dizer que nesse intervalo , nós temos a nossa raiz. No entanto, nós precisamos de um intervalo de comprimento , para alcançarmos isso, vamos ter que testar alguns valores (sim, vai ser chato mesmo):
Bom, temos um novo intervalo com comprimento de 0,1, que é esse aqui:
Testando outros valores para acharmos um intervalo de comprimento , temos:
Agora sim, temos um novo intervalo de comprimento :
Como nós já havíamos discutido antes, o ponto médio desse intervalo será a raiz que nós procuramos, com um erro de no máximo, . Assim,
Infelizmente, a questão não acaba por aqui porque ainda temos que encontrar a outra raiz, mas vai ser rápido, eu juro.