Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.Revisão - Ex. 43
Um avião está voando a uma velocidade de 300 km/h, a uma altitude de 4 km. Se um observador está no chão, ache a taxa de variação no tempo da medida do ângulo de elevação do avião em relação ao observador, quando ele está sobre um ponto do solo a 2 km do observador.
Passo 1
Esse vai ser um problema de taxas relacionadas, a primeira coisa a tentar se fazer neste tipo de questão é um esboço do que está acontecendo, olhem na imagem abaixo como facilita o entendimento.
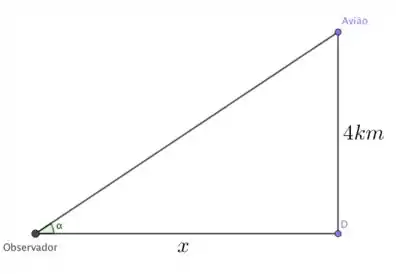
Temos o avião a uma altitude de 4 km, um observador a uma distância de um ponto D que é a projeção da sombra do avião e o ângulo de elevação do do avião em relação ao observador. Queremos a taxa de variação deste ângulo quando o .
Precisamos descobrir e temos a velocidade do avião, que é a taxa de variação do nosso em relação ao tempo. Já que ele mantém a mesma altitude, sua trajetoria é horizontal. Sendo assim, .
Passo 2
Precisamos descobrir uma expressão para Para achar , temos das relações trigonométricas:
Então .
Passo 3
Para achar precisamos derivar implicitamente a expressão de em relação ao tempo. Vamos então tomar a derivada de ambos os lados:
Agora devemos lembrar que em que é uma função. Aplicando a fórmula, ficamos com:
Lembre-se que derivamos acima implicitamente em relação a . Chegamos então em:
Passo 4
Agora vamos substituir .
Passo 5
Nesta etapa vamos substituir o , que é quando o avião está sobre um ponto do solo a 2 km do observador. Sendo assim, quando
Daí a taxa de variação no tempo da medida do ângulo de elevação do avião em relação ao observador é decrescente à taxa de rad/h.
Resposta
Decrescente à taxa de rad/h