Em cada um dos problemas de 5 a 18:
(a) Determine todos os pontos críticos do sistema de equações dado.
(b) Encontre o sistema linear correspondente perto de cada ponto crítico.
(c) Encontre os autovalores de cada sistema linear. O que você pode concluir sobre o sistema não linear?
(d) Desenhe um retrato de fase do sistema não linear para confirmar suas conclusões, ou para estendê-las nos casos em que o sistema linear não fornece informações definidas sobre o sistema não linear.
9)
Passo 1
d)Note que as direções do campo corresponde com as conclusões retiradas dos itens anteriores.
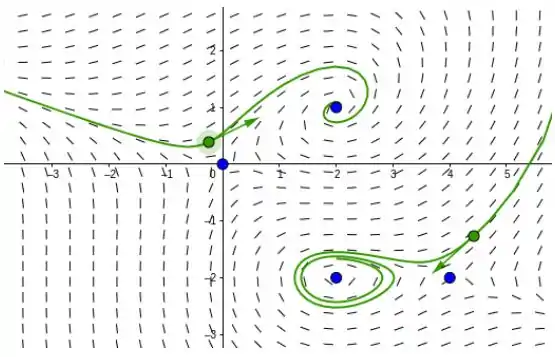
Resposta
Ei, a resposta está no passo a passo :)