Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.Revisão - Ex. 23

Calcule a integral efetuando uma substituição trigonométrica apropriada.

∫ d x x 2 - 1

Passo 1

Como no denominador a gente tem algo parecido com x 2 - a 2 , com a = 1 , vamos usar a substituição:

x = a sec ⁡ θ = sec ⁡ θ

d x d θ = t g   θ sec ⁡ θ ∴ d x = t g   θ sec ⁡ θ d θ

A integral fica assim:

∫ 1 sec 2 ⁡ θ - 1 t g   θ sec ⁡ θ d θ

Sabendo que:

sec 2 ⁡ θ - 1 = t g 2 θ

Podemos reescrever a integral assim:

∫ 1 t g 2 θ t g   θ sec ⁡ θ d θ = ∫ sec ⁡ θ d θ = ln ⁡ sec ⁡ θ + t g   θ

Passo 2

Mas a nossa integral estava em função de x . Então a gente tem que voltar para essa variável. Usamos a substituição:

x = sec ⁡ θ ∴ x 1 = 1 cos ⁡ θ ∴ θ = a r c c o s   1 x

Desenhando o triângulo retângulo com essa característica, e usando Pitágoras para achar o lado que falta:

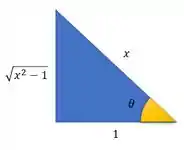
Daí a gente pode tirar que:

sec ⁡ θ = 1 cos ⁡ θ = x 1 = x

t g   θ = x 2 - 1

Substituindo esses valores na nossa resposta:

∫ d x x 2 - 1 = ln ⁡ sec ⁡ θ + t g   θ = ln ⁡ x + x 2 - 1 + C

E lembrando que precisamos colocar a constante de integração, já que a integral é indefinida.

Resposta

ln ⁡ x + x 2 - 1 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida: ∫ 1 - 4 t 2 3 2 d t
Calcule a integral indefinida: ∫ 1 + x 2 x 3d x
Calcule a integral indefinida: ∫ x + 1 2 x 2 + 1 d x
Calcule a integral indefinida: ∫ x 2 2 - x 2d x
Calcule a integral indefinida: ∫ x + 1 4 - x 2d x