Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 1b

Calcule int_C f d s , onde

b ) f (x , y) = x^2 - y^2 e C é a circunferência x^2 + y^2 = 4 .

Passo 1

E aí, galerinha!! Vamo que vamo com o Responde Aí em mais um exercício!! :D

Para calcularmos a integral de linha, precisamos parametrizar a nossa função. Nossa curva, então, tem a forma:

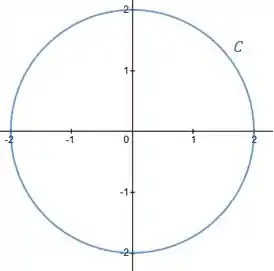
Visto que ela representa uma circunferência, a parametrização vai ser dada através da substituição por funções trigonométricas, tal que:

x = rho cos t

E:

y = rho s e n t

Onde rho é o raio da circunferência e, então:

{[[x = 2 cos t],[y = 2 s e n t]])

Dessa forma, a curva pode ser escrita como:

C : sigma (t) = (2 cos t , 2 s e n t) , 0 <= t <= 2 pi

Assim, uma curva parametrizada terá sua integral dada por:

int_C f d s = int f (sigma (t)) * ||sigma^' (t)|| d t

E a nossa curva terá o valor:

C : sigma^' (t) = (- 2 s e n t , 2 cos t)

Ou seja:

C : ||sigma^' (t)|| = sqrt((- 2 s e n t)^2 + (2 cos t)^2) = sqrt(4 s e n^2 t + 4 cos^2 t)

Juntando os termos semelhantes:

C : ||sigma^' (t)|| = sqrt(4 (s e n^2 t + cos^2 t))

Vamos aplicar a identidade trigonométrica:

s e n^2 u + cos^2 u = 1

Para obter:

C : ||sigma^' (t)|| = sqrt(4) = 2

Passo 2

Então, nossa integral pode ser escrita como:

int_C f d s = int_C (x^2 - y^2) d s

Ou seja:

int_C (x^2 - y^2) d s = int_0^(2 pi) ((2 cos t)^2 - (2 s e n t)^2) (2) d t

=> 2 int_0^(2 pi) (4 cos^2 t - 4 s e n^2 t) d t = 8 int_0^(2 pi) (cos^2 t - s e n^2 t) d t

Se usarmos as identidades trigonométricas:

cos (2 u) = cos^2 u - s e n ² u

Nossa integral será dada por:

8 int_0^(2 pi) cos (2 t) d t

E resultará em:

8 int_0^(2 pi) cos (2 t) d t = 8 (s e n (2 t))/(2) | [[2,pi],[0]]

=> 4 s e n (2 t) | [[2,pi],[0]]

Passo 3

Agora, substituindo os intervalos de integração:

4 s e n (2 t) | [[2,pi],[0]] = 4 [s e n (4 pi) - s e n (0)]

Teremos o resultado:

=> 4 [0 - 0] = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o valor da integral de linha, onde C é a curva dada.
Calcule a integral de linha, onde C é a curva dada. ∫ C y xd s C : x = t 4 ,y = t 3 , 1 2 ≤ t ≤ 1
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = cos 3 ⁡ t , y = s e n 3 t no primeiro quadrante.
Calcule a integral de linha, onde C é a curva dada. ∫ C yd s C : x = t 2 ,y = t ,0 ≤ t ≤ 2
29- Se C é a curva com equações paramétricas x = ln ⁡ t , y = e - t , 1 ≤ t ≤ 2 , use uma calculadora ou CAS para calcular a integral de linha ∫ C xs e nyd s com precisão até a terceira casa decimal.