Uma câmera de televisão está posicionada a 4000 pés de uma base de lançamento de foguete. O ângulo de elevação da câmera deve variar a uma taxa qua possa focalizar o foguete. O mecanismo de foco da câmera também deve levar em conta o aumento da distância entre a câmera e o foguete em subida. Vamos supor que o foguete suba verticalmente e com uma velocidade de 600 pés/s quando já estiver subido 3000 pés. Quão rápido está variando a distância da câmera ao foguete nesse momento? Se a câmera de televisão apontar sempre em direção ao foguete, quão rápido estará variando o ângulo de elevação dela nesse mesmo momento?
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??
Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que tem uma câmera vai acompanhar o movimento do foguete em lançamento, e nos pede a variação da distância e a variação do ângulo.
Vamos fazer um esqueminha para entender o que está acontecendo.
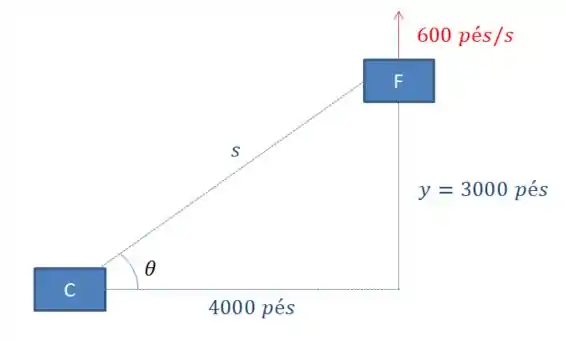
Queremos encontrar aqui a variação da distância do foguete até a câmera:
E também queremos encontrar a variação do ângulo , isso é:
Para isso vamos usar Pitágoras e vamos usar alguma relação de seno, cosseno ou tangente.
Passo 2
Nosso primeiro passo vai ser usar o teorema de Pitágoras:
(Perceba que só é constante, os outros valores que são a altura e a distância são variáveis).
Podemos fazer a derivada direta:
Arrumando para temos:
Agora, como sabemos que:
Temos:
Falta encontrarmos a distância quando Usando o Pitágoras do início, temos:
O que resulta em:
Portanto,
Passo 3
Com a nossa variação da distância calculada, vamos encontrar agora a taxa de variação do ângulo .
Podemos dizer que o ângulo possui a seguinte tangente, que é dada pelo cateto oposto sobre o cateto adjacente.
Derivando em ambos os lados, temos:
Lembrando que:
Que para o nosso caso, temos:
Nesse momento, temos , logo:
Substituindo na expressão com a variação do ângulo, temos:
E resolvendo, temos que: