Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 31

Um cilindro circular reto é inscrito em uma esfera de raio r . Encontre o maior volume possível para este cilindro.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar o maior volume possível para um cilindro inscrito em uma esfera de raio r .

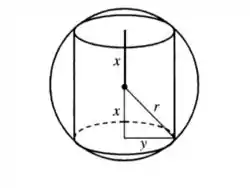
Isso significa que precisamos maximizar o volume do cilindro, então precisamos de uma expressão que represente esse volume. Para encontrar essa expressão, vamos partir do triângulo retângulo (Teorema de Pitágoras) formado na figura, que nos fornece a equação:

r 2 = x 2 + y 2 .

Além disso, a gente sabe que o volume de um cilindro é dado por V = π r 2 h , onde r é o raio e h é a altura do cilindro. No nosso caso, podemos descrever esse raio como y e sua altura como 2 x , repare na figura. Assim, vamos ter que a fórmula para o volume é dada por:

V ( x ,   y ) = π y 2 2 x .

Observe que podemos isolar y na primeira equação e substituir na equação do volume pra, então, encontrar seus pontos críticos e consequentemente as dimensões que fazem esse cilindro ser o maior possível.

Vamos lá 😁!

Passo 2

Usando a relação de Pitágoras do triângulo retângulo, vista no Passo 1 , vamos isolar y para obter:

y 2 = r 2 - x 2 .

Substituindo y na fórmula do volume, para termos uma função dependente apenas de uma variável, vamos ter:

V ( x ) = π r 2 - x 2 2 x .

Aplicando a propriedade distributiva nesse produto:

V ( x ) =   2 π r 2 x - 2 π x 3 .

Agora vamos maximizar esse volume!

Passo 3

Precisamos calcular a derivada da função

V ( x ) =   2 π r 2 x - 2 π x 3

para encontrar os seus pontos críticos. Para isso, vamos usar a Regra da Potência em cada um dos seus termos. Relembrando a Regra da Potência:

d d x x n = n x n - 1 .

Então, derivando a equação do volume em relação a x vamos ter:

V ' x = 2 π r 2 - 6 π x 2 .

Igualando essa expressão a zero, temos:

2 π r 2 - 6 π x 2 = 0 ,

ou seja,

6 π x 2 = 2 π r 2 .

Isolando x , temos que

x 2 = r 2 3 ,

logo, tomando a raiz:

x = r 3 .

Encontramos o valor de x que maximiza a nossa função!

Passo 4

Como vale a relação

y 2 = r 2 - x 2 ,

então substituindo o valor encontrado para x nesta equação, teremos:

y 2 = r 2 - r 2 3 ,

ou seja,

y 2 = 2 r 2 3 .

Passo 5

Finalmente, vamos encontrar o volume do cilindro.

Como

V x ,   y = π y 2 2 x ,

então substituindo x e y 2 nessa equação, temos que:

V = π 2 r 2 3 2 r 3 .

Simplificando:

V = 4 π r 3 3 3 .

Dessa forma, o maior volume possível de um cilindro circular reto inscrito em uma esfera de raio r é 4 π r 3 3 3 .

Valeu, galera.

Até a próxima! 😉

Resposta

O maior volume possível para o cilindro inscrito em uma esfera de raio r é:

V = 4 π r 3 3 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 39 a 42, uma partícula move-se ao longo de uma reta de acordo com a equação dada, onde s cm é a distância orientada da partícula até a origem, em t s. (a) Qual será a velocidade da p
Quando um pêndulo com 10 cm de comprimento balança, de modo que θ seja a medida em radianos do triângulo formado pelo pêndulo e uma reta vertical, então, se h θ cm for a altura da extremidade do pêndu
Ache uma equação da reta tangente à curva y = ( x 2 - 1 ) 2 em cada um dos seguintes pontos - 2 ,9 , - 1 ,0 ,0 ,1 ,1 ,0e( 2 ,9 ) . Faça um esboço do gráfico e desenhe segmentos das retas tangentes nos
A equação de demanda para um brinquedo é p 2 x = 5000 , onde x brinquedos são demandados por mês, quando p for o preço de cada unidade. Espera-se que em t meses, onde t ∈ [ 0,6 ] , o preço do brinqued
Em uma floresta, um predador alimenta-se de sua presa, e a população de predadores em qualquer época é uma função do número de presas naquele momento. Suponha que quando há x presas na floresta, a pop