Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva
que está mais próximo do ponto
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão da pra gente a curva
E pede pra gente encontrar as coordenadas dessa curva que estão mais próximas do ponto .
Para fazer isso, temos que lembrar que a distância entre um ponto e um ponto é dada pela relação:
Assim, substituiremos pelo ponto da curva que chamaremos de , e pelo ponto .
Depois vamos procurar o valor mínimo de , já que queremos o ponto da curva mais próximo do ponto . Ou seja, já que queremos a menor distância.
E para isso faremos a derivada de , sendo igual a zero. Ou seja:
Mas aqui temos um “pulo do gato”: essa expressão de não é muito fácil de se derivar, então usaremos o fato de que o mínimo de acontece no mesmo ponto em que o mínimo do seu quadrado acontece, porém é mais fácil lidar com . Sendo assim, chamaremos de , e faremos:
Depois, basta procurar o ponto em que
Sacou a ideia?
Então vem comigo que te mostro tudo isso acontecendo no passo a passo.
Passo 2
Vamos começar traçando o gráfico da nossa curva
Para entender melhor o que estamos procurando.
Seja o gráfico de dado por
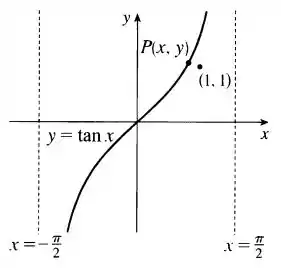
A distância de um ponto arbritrário para o ponto é dada por
Mas vamos trabalhar com o quadrado da distancia, como sendo:
Agora, substituindo pela expressão da curva que foi dada no enunciado, ficamos com
Passo 3
Para encontrarmos o ponto de mínimo de , basta derivarmos essa expressão e igualarmos a zero. Sendo:
Sua derivada será calculada usando a regra da cadeia em cada termo. o que nos dará:
Agora, vamos procurar o valor de para que:
Assim:
E com a ajuda de uma calculadora gráfica, teremos:
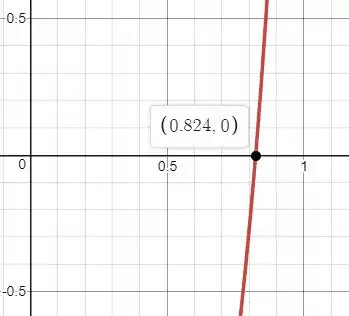
Podemos ver que
quando
Maravilha, agora calculando através desse valor de , teremos:
Então, temos que o ponto mais próximo do ponto que értence a curva é o ponto
Resposta
O ponto mais próximo do ponto é o ponto