Estão dados os gráficos da função posição de dois corredores, e que correm metros rasos e terminam empatados.
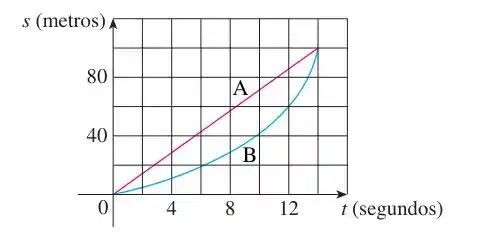
- Descreva e compare como os corredores correram a prova.
- Em que instante a distância entre os corredores é maior.
- Em que instante eles têm a mesma velocidade.
Passo 1
Eaee, belezinha?? Bom.... o enunciado nos deu o seguinte gráfico que mostra a função posição de dois corredores, e que correm metros rasos e terminam empatados:
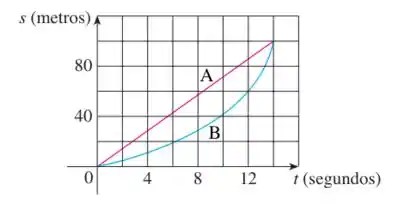
Queremos descrever e comparar como os corredores correram a prova.
Também queremos saber o instante a distância entre os corredores é maior.
Por fim, iremos analisar em qual instante eles têm a mesma velocidade.
Para isso, sabemos que estamos observando os gráficos da posição em relação ao tempo aqui.
E a partir daí que iremos tirar as informações sobre a velocidade e aceleração dos corredores.
Passo 2
Letra a)
Bom... o corredor correu linearmente, ou seja, ele manteve uma velocidade constante durante toda a prova pois vemos que o seu deslocamente foi constante em relação ao tempo.
Já o corredor teve um crescimento exponencial em sua velocidade, ou seja, ele começou a prova mais lento e foi aumentando sua velocidade com o decorrer do tempo.
Note que essas informações foram obtidas analisando a taxa de variação das curvas, ou seja, a inclinação da reta tangente.
Como a curva do corredor é uma reta, ela possui a mesma tangente durante todo seu domínio.
Já a curva do corredor é uma parábola, ou seja, a inclinação da reta tangente dessa curva vai aumentando conforme aumenta, por isso podemos concluir que sua velocidade foi aumentando.
Passo 3
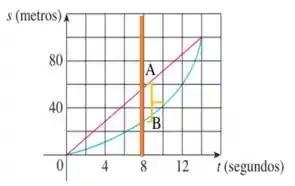
Letra b)
Para saber em que instante a distância entre os corredores é maior, basta pensarmos em traças retas verticais entre as duas curvas.
A reta que possuir uma maior distância entre as curvas será a reta que estamos buscando e o ponto onde esssa reta cortar o eixo será o instante desejado.
Analisando o gráfico, podemos concluir que no instante a distância entre os corredores foi maior:
Passo 4
Letra c)
Agora queremos analisar em qual instante eles têm a mesma velocidade.
Eles possuíram a mesma velocidade no instante em que suas retas tangentes possuírem a mesma inclinação.
E isso se dá em , veja:
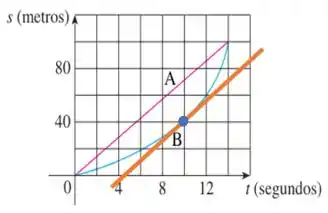
Podemos ver isso geometricamente, pois ao tirarmos uma reta paralela à reta , ela encontra a curva no ponto .
Vale aqui lembrar a relação entre a velocidade e o deslocamento.
A velocidade é a deridada do espaço em relação ao tempo, sendo assim a velocidade é a inclinação que estamos comentando no paragrafo anterior.
Resposta
- O corredor A correu linearmente, ou seja, ele manteve uma velocidade constante durante toda a prova. Já o corredor B, ele teve um crescimento exponencial em sua velocidade, ou seja, ele começou a prova mais lento e foi aumentando sua velocidade com o decorrer do tempo.
- .
- .