Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 27

No Exemplo 4 consideramos um membro da família de funções f x = sin ⁡ ( x + sin ⁡ c x ) que ocorre na síntese de FM. Aqui investigamos a função com c = 3 . Comece fazendo o gráfico de f na janela inspeção [ 0 , π ] por { - 1,2 ,   1,2 ] .Quantos pontos de máximo locais você pode ver? O gráfico tem mais informações do que podemos perceber a olho nu. Para descobrir os pontos de máximo e mínimo escondidos será necessário examinar muito cuidadosamente o gráfico f ' . De fato, ajuda examinar ao mesmo tempo o gráfico de f ' ' . Encontre todos os valores máximo e mínimo e os pontos de inflexão. Então faça o gráfico de f na janela retangular [ - 2 π , 2 π ] por [ - 1,2 ,   1,2 ] e comente sobre a simetria.

Passo 1

Bom galera, nessa questão queremos encontrar todos os valores de máximo e mínimo e os pontos de inflexão do membro da família de funções.

f x = sin ⁡ x + sin ⁡ c x

Para isso, iremos fazer gráficos da função na janela de inspeção para auxiliar a ver os pontos. Devemos também esboçar um gráfico na janela retangular [ - 2 π , 2 π ] por [ - 1,2 ,   1,2 ] .

Passo 2

Fazendo o gráfico de f ( x ) , f ' ( x ) e f ' ' ( x ) , temos

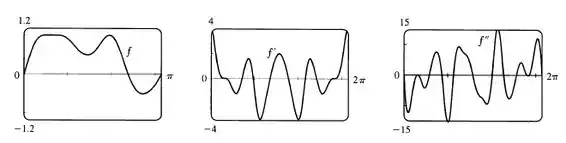
Olhando para o gráfico de f ( x ) , podemos ver dois pontos de máximo e dois pontos de mínimo. Vendo o gráfico de f ' ' ( x ) , podemos concluir que f ' ' ( x ) cruza o eixo x em dois pontos próximos a x = 0.65 , mostrando que muda de concavidade em um curto intervalo. No gráfico de f ' ( x ) , podemos ver uma mudança de sinal que ocorre três vezes próximo a x = 0.65 , indicando que possuímos três valores, dois de máximo e um de mínimo. Os valores de máximo são f 0.59 = 1 e f 0.68 = 1 e o valor de mínimo é f 0.64 = 0.99996 . Também temos valores de máximo em f 1.96 = 1 e de mínimo em f 1.46 = 0.49 e f 2.73 = - 0.51

Passo 3

Os pontos de inflexão estão em ( 0.61 ,   0.099998 ) , ( 0.66 ,   0.99998 ) , ( 1.17 ,   0.72 ) , ( 1.75 ,   0.77 ) e ( 2.28 ,   0.34 ) em torno de [ 0 ,   π ] .

Em [ π ,   2 π ] , os pontos estão em ( 4.01 ,   - 0.34 ) , ( 4.54 ,   - 0.77 ) , ( 5.11 ,   - 0.72 ) , ( 5.62 ,   - 0.99998 ) e ( 5.67 ,   - 0.99998 ) .

Aumentando a janela gráfica e fazendo o gráfico de - 2 π até 2 π vemos que a função é periódica com período 2 π e simétrica em relação ao eixo y .

Resposta

Os valores de máximo são f 0.59 = 1 e f 0.68 = 1 e o valor de mínimo é f 0.64 = 0.99996 . Também temos valores de máximo em f 1.96 = 1 e de mínimo em f 1.46 = 0.49 e f 2.73 = - 0.51

Os pontos de inflexão estão em ( 0.61 ,   0.099998 ) , ( 0.66 ,   0.99998 ) , ( 1.17 ,   0.72 ) , ( 1.75 ,   0.77 ) e ( 2.28 ,   0.34 ) em torno de [ 0 ,   π ] .

Em [ π ,   2 π ] , os pontos estão em ( 4.01 ,   - 0.34 ) , ( 4.54 ,   - 0.77 ) , ( 5.11 ,   - 0.72 ) , ( 5.62 ,   - 0.99998 ) e ( 5.67 ,   - 0.99998 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace ou copie o gráfico de f . (Suponha os eixos da mesma escala). Use então o método do Exemplo 1 para esboçar o gráfico de f ' .
Estime os intervalos de concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' ' . f x = x + 1 3 ( x 2 + 5 ) ( x 3 + 1 ) ( x 2 +
Estime os intervalos de concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' ' . f x = x 3 - 10 x + 5 x 2 + 4
Obtenha os gráficos de f que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores
Obtenha os gráficos de f que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores