Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.Exercícios práticos - Ex. 5

Nos Exercícios 5-8, encontre o domínio e a imagem da função dada e identifique suas superfícies de nível. Esboce uma curva de nível típica.

f x , y , z = x 2 + y 2 - z

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de derivadas parciais.

Vamos agora resolver os exercícios práticos sobre domínio, imagem e curvas de nível.

A partir do enunciado, observa-se que:

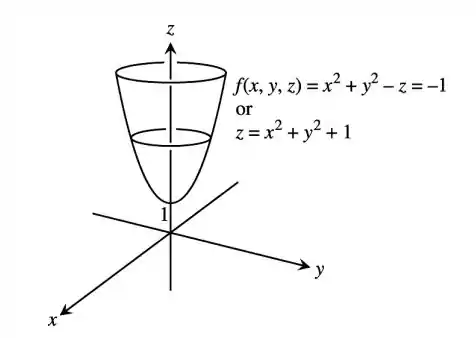
D o m í n i o : T o d o s   o s   p o n t o s   x ,   y ,   z   n o   e s p a ç o

I m a g e m : T o d o s   o s   n ú m e r o s   r e a i s

Superfícies de nível são parabolóides de revolução com o eixo z como eixo.

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Mostre que f(x, y, z) = x + y – z é contínua em qualquer ponto (x0, y0, z0).
Mostre que f(x, y, z) = x2 + y2 + z2 é contínua na origem.
Encontre os limites nos Exercícios 9-14.underset(P - ( 1 , - 1 , e ))(lim) ln |x + y + z|
Encontre os limites nos Exercícios 9-14.underset(( x , y ) - ( pi , ln 2 ))(lim) e^y cos x
Encontre os limites nos Exercícios 9-14.underset(( x , y ) - ( 0 , 0 ))(lim) (2 + y)/(x + cos y)