Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas de grade que têm constante e quais têm constante.
Passo 1
Fala, pessoal! De boa?
Aqui temos que usar um software para traçar o gráfico da superfície parametrizada por:
Com as restrições:
E:
Para isso, vamos usar o software GeoGebra.
Depois, vamos entender quais curvas de grade da nossa superfície tem a variável como constante e quais tem .
Passo 2
Usando a função superfície do GeoGebra com o seguinte input:

Conseguimos o gráfico:
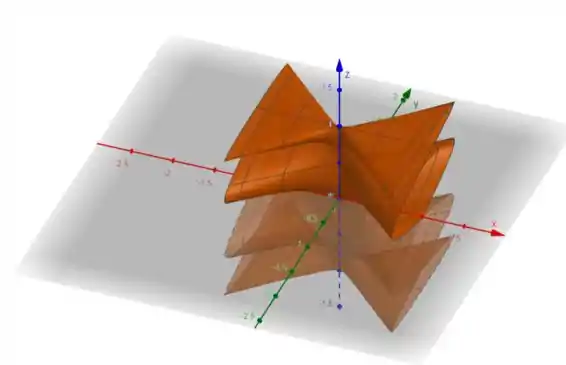
Passo 3
Entendendo as linhas de grade:
- constante:
- constante:
(constante)
(varia)
(varia)
Padrão de onda (gráfico de seno) ao redor de e
(varia)
(varia)
(constante)
Padrão de onda (gráfico de seno e cosseno) ao redor de e

constante
constante
Resposta
Gráfico.