Mostre que a curva polar (chamada conchoide) te a reta como uma assíntota vertical mostrando que . Use esse fato para ajudar a esboçar o conchoide.
Passo 1
Olá galera! Preparados para resolver esta questão?
Vamos fazer o seguinte. Vou te passar alguns passos que irão te ajudar a desenvolver a questão.
1 – Podemos colocar a equação polar em cartesiana.
2 – Analisar o limite de quando
3 – Verificar a Assíntota.
4 – Fazer o esboço da curva.
Eai? Vamos começar!!!
Passo 2
A curva polar que ele nos deu foi:
Escrevendo em função de :
como :
Logo,
Isolando o :
Para simplificar, vamos dividir toda expressão por .
Passo 3
Agora vamos dar uma olhada no limite que ele nos disse.
Assim,
Quando tende para o infinito, a expressão tende a zero. Isso ocorre porque à medida que se torna muito grande, o valor de diminuir e se aproxima de zero. Assim,
Assim, vemos que será uma assíntota vertical para nossa curva
Passo 4
Esboçando o gráfico, temos:
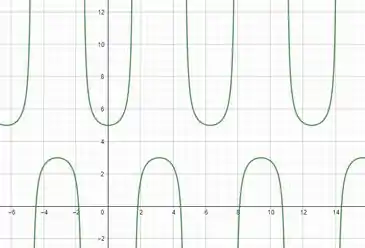
Resposta