Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 71
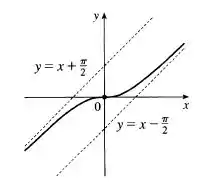
Mostre que a curva
tem duas assíntotas oblíquas:
e
Use esse fato para esboçar a curva.
Passo 1
Fala aí, tudo certinho com você?
Bom, nessa questão queremos mostrar que a função
possui duas assíntotas oblíquas, em:
e
E usar esse fato para traçar o esboço de seu gráfico.
Para isso, devemos lembrar que as assíntotas oblíquas acontecendo quando:
Onde é a equação da assíntota oblíqua. Então é isso que faremos.
Vem que te mostro como!
Passo 2
Nosso enunciado disse que a função
possui duas assíntotas oblíquas, em:
e
E para ver se isso é realmente verdade, vamos verificar se
Assim, basta substituirmos a função e cada uma das retas para calcular o limite e verificar se ele realmente é igual a zero.
Sendo assim, na primeira curva, teremos:
Resolvendo o seguinte limite, temos
Assim, o limite se torna:
Dessa forma, é uma assíntota oblíqua a .
Resolvendo para a segunda curva, teremos o seguinte limite, temos
Assim, teremos:
Dessa forma, é uma assíntota oblíqua a .
Perfeito.
Passo 3
Agora vamos encontrar mais algumas informações que nos ajude a traçar o gráfico dessa função.
Podemos analisa a derivada da função, para saber onde ela é crescente, onde é decrescente e se tem pontos de máximos e mínimos, já que:
Derivando em relação a , temos
Ou melhor:
Como para todos os valores de , então nossa função está crescendo em todos os pontos.
Também podemos estudar a segunda derivada para sabermos mais sobre sua concavidade e ponto de inflexão, já que:
Derivando em relação a , temos
Como para todos os valores de , então nossa função possui concavidade para baixo em e concavidade para cima em .
A função não possui pontos críticos, portanto não possui valores de máximo e mínimo e é simétrica em relação à origem. O único ponto de inflexão está em .
Passo 4
Juntando todas as informações, teremos o seguinte gráfico:
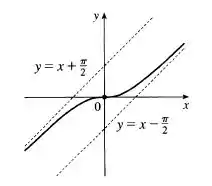
Resposta
