Uma piscina tem de largura por de comprimento, de profundidade na parte rasa, e na parte mais funda. Uma secção transversal está mostrada na figura. Se a piscina for preenchida a uma taxa de , quão rápido estará subindo o nível da água quando a sua profundidade no ponto mais profundo for de ?
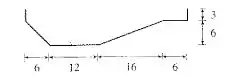
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que essa piscina tem esse formato doidão onde as bordas têm dimensão de (comprimento) e (largura) e que está enchendo tudo com água a uma taxa de , e nos pede a velocidade que que a altura da água está quando o nível de água está à altura é de .
Tem ideia de como fazemos isso?
Bom, foi dada a taxa de enchimento em volume de água e queremos a taxa de variação da altura da água em um certo ponto.
O que podemos fazer é desenvolver uma função que descreva o volume de água em função da altura e a partir dessa função, aplicamos a derivada em função do tempo e substituímos os valores dados.
Parece complicado? Veja só!
Passo 2
Nosso primeiro passo vai ser achar o volume da piscina...
Queremos a velocidade da altura da água quando , então podemos desconsiderar aquela parte de cima da piscina e trabalhar apenas com aquela parte mais funda.
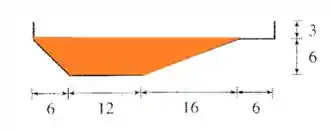
Perceba que a área lateral é uma forma de trapézio, portanto o volume dessa região será a area desse trapézio multiplicado pela largura da piscina.
A área do trapézio é dada pela base maior base menor · altura , ou seja, a base maior é e a base menor é
A largura foi dado no enunciado como ...
Perceba que não substituímos e pois não estamos calculando exatamente o volume da piscina, mas sim o volume de água na piscina... esses valores não são constantes conforme a piscina enche, então temos que tratá-los como variáveis...
Tranquilo até aqui?
Passo 3
Temos que reescrever em função de pois não estamos interessados na base maior, mas sim na altura .
Por semelhança de triângulos, teremos:
Onde é a posição da parede da esquerda até a parte mais baixa, yé do final da parte mais funda até a parede da direita e é a altura da base .
Substituindo em , temos
Show?
Passo 4
Conseguimos desenvolver a função volume em relação a altura... agora derivamos em relação ao tempo para determinar a taxa de variação da altura...
é uma função do tempo, então na derivada de vamos aplicar a regra da cadeia.
Substituindo em
Queremos encontrar a variação de no tempo, então vamos isolá-lo em um lado da igualdade
No enunciado foi dado que e queremos a variação da altura quando , logo
E aí! o que achou? Responde Aí!