Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.6 - Ex. 1

Prove a comutatividade, a distributividade e a associatividade para a convolução.

( a )   f * g = g * f

( b )   f * ( g 1 + g 2 ) = f * g 1 + f * g 2

( c )   f * ( g * h ) = ( f * g ) * h

Passo 1

Comece usando a definição da convolução integral f ∗ g.

f * g = ∫ 0 t f ( t - τ ) g ( τ ) d τ

Faça a substituição ξ   =   t   -   τ . Então d ξ   =   − d τ .

f * g = ∫ t 0 f ( ξ ) g ( t - ξ ) ( - d ξ )

Use o sinal de menos para mudar os limites da integração.

f * g = ∫ 0 t f ( ξ ) g ( t - ξ ) d ξ = ∫ 0 t g ( t - ξ ) f ( ξ ) d ξ = g * f

Passo 2

Comece usando a definição da integral de convolução f   ∗   ( g 1   +   g 2 ) .

f * g = ∫ 0 t f ( t - τ ) [ g 1 ( τ ) + g 2 ( τ ) ] d τ = f * g 1 + f * g 2

Passo 3

Comece usando a definição da convolução integral f   ∗   ( g   ∗   h ) .

f * ( g * h ) = ∫ 0 t f ( t - τ ) ( g * h ) ( τ ) d τ = ∫ 0 t ∫ 0 τ f ( t - τ ) g ( τ - ξ ) h ( ξ ) d ξ d τ

Queremos fazer a substituição u   =   τ   -   ξ   para que g seja em termos de uma única variável. Fazer isso agora, no entanto, fará h em termos de mais de uma variável, porque d ξ   é o primeiro. Nosso objetivo, então, é mudar a ordem da integração para fazer com que τ seja o primeiro. O modo atual de integração no plano τ - ξ é mostrado abaixo, à esquerda.

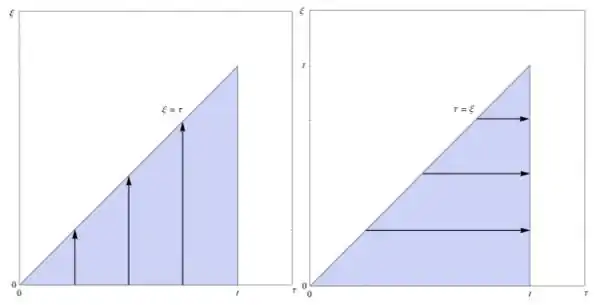
Integre esse domínio, conforme mostrado à direita, para alternar a ordem de integração.

f * ( g * h ) = ∫ 0 t ∫ ξ t f ( t - τ ) g ( τ - ξ ) h ( ξ ) d τ d ξ

Agora faça a substituição u = τ - ξ . Então d u   =   d τ .

f * ( g * h ) = ∫ 0 t ∫ 0 t - ξ f ( t - ξ - u ) g ( u ) h ( ξ ) d u d ξ = ( f * g ) * h

Resposta

  1. f * g = ∫ 0 t f ( ξ ) g ( t - ξ ) d ξ = ∫ 0 t g ( t - ξ ) f ( ξ ) d ξ = g * f
  2. f * g = ∫ 0 t f ( t - τ ) [ g 1 ( τ ) + g 2 ( τ ) ] d τ = f * g 1 + f * g 2
  3. f * ( g * h ) = ∫ 0 t f ( t - τ ) ( g * h ) ( τ ) d τ = ∫ 0 t ∫ 0 τ f ( t - τ ) g ( τ - ξ ) h ( ξ ) d ξ d τ
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral.13. L t ∫ 0 t s e nτ d τ
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral.15. L 1 * t 3
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral. L { t 2 * t 4 }
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral. L { t 2 * t . e t }
Prove a propriedade comutativa da convolução f * g = g * f