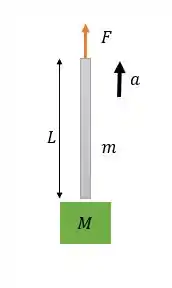
Um bloco de massa é amarrado na extremidade inferior de uma corda de massa m e comprimento . Uma força constante é aplicada de baixo para cima na extremidade superior da corda, fazendo com que o bloco e a corda sejam acelerados para cima. Ache a tensão na corda a uma distância da sua extremidade superior, onde pode ter qualquer valor entre e .
Passo 1
Oi, galerinha! A situação que temos é de um bloco de massa sendo erguido por uma corda de massa e de comprimento .
O enunciado diz que uma força constante é aplicada de baixo para cima na extremidade superior da corda, fazendo com que o bloco e a corda sejam acelerados para cima.
Queremos encontrar a tensão na corda a uma distância da sua extremidade superior, onde pode ter qualquer valor entre e .
Para isso, devemos aplicar a segunda lei de Newton para a corda+bloco para encontrar uma aceleração.
Lembrando que essa Lei é dada da seguinte forma:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Vamos desenhar um sisteminha do que está acontecendo:
No topo da corda, temos que: ;
Na parte inferior da corda, temos que:
Onde, é a aceleração da gravidade e é aceleração com que o bloco é puxado para cima.
Bora seguindo!
Passo 3
Vamos considerar a corda e o bloco como um único objeto, a fim de calcular a aceleração.
Vamos esboçar um diagrama de corpo livre para enxergarmos melhor e então, aplicaremos a segunda lei de Newton sobre esse objeto:
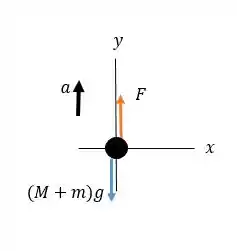
Passo 4
Pela segunda lei de Newton, temos:
Substituindo as forças que estão atuando no corpo:
Passo 5
Agora vamos considerar as forças em uma seção da corda que se estende a distância abaixo do topo.
A tensão na parte inferior desta seção é e a massa é .
E então, vamos esboçar o diagrama de corpo livre dessa situação:
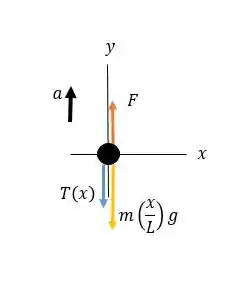
E vamos aplicar a segunda lei de Newton:
Passo 6
Vamos usar a equação da da aceleração que encontramos e combina-la com esta ultima:
Para : A expressão fornece o valor correto de .
Para : A expressão fica , e quando usamos a expressão para vemos que isso acontece.