Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 4ª Edição - Herch Moysés Nussenzveig- Ed: 4º - Capítulo 12.Problemas - Ex. 9

Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Determine (a) a aceleração a do sistema; (b) as tensões T e T ' nos fios ligados a m e m ' .

Passo 1

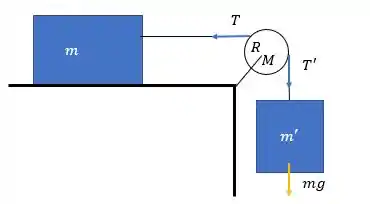
Primeiramente, vamos considerar que o sistema está acelerado para baixo. Escrevendo as equações de Newton para os blocos:

m ' g - T ' = m ' a T = m a     ( i )

Para a polia, podemos calcular o momento com relação ao seu centro, logo:

τ = T ' ⋅ R - T ⋅ R

Logo,

τ = ( T ' - T ) ⋅ R

Passo 2

Mas a gente sabe que τ = I α , então vamos usar isso!

T ' - T ⋅ R = I α

Como a = α R e I = M R 2 / 2 :

T ' - T ⋅ R = M R 2 2 ⋅ a R     i i

Isolando as trações no sistema ( i ) e substituindo em ( i i ) :

m ' g - m ' a - m a ⋅ R = M R 2 2 ⋅ a R

Isolando o a , temos:

a = m ' g m ' + m + M / 2

Passo 3

Por último, podemos calcular as trações. De ( i ) :

T = m a → T = m ⋅ m ' g m ' + m + M / 2

E para T ' :

T ' = m ' g - a

Logo,

T ' = m ' ⋅ ( m + M / 2 ) g m ' + m + M / 2

Resposta

a = m ' g m ' + m + M / 2

T = m ⋅ m ' g m ' + m + M / 2

T ' = m ' ⋅ ( m + M / 2 ) g m ' + m + M / 2

Ver Outros Exercícios desse livro