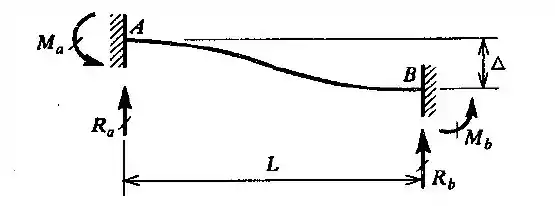
Uma das extremidades de uma viga biengastada tem um desnível em relação à outra (ver a figura). Calcular as reações.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Conforme dito pelo livro, precisamos resolver esta questão pelo método da superposição. Mas como faremos isto? Bom, vamos acompanhar o raciocínio abaixo.
Vamos substituir supor que o momento e a força são atuantes no nosso problema.
Por causa do engastamento lá na extremidade , sabemos que .
Agora, a diferença está na deflexão da viga. Aqui teremos
Agora, basta utilizarmos este conhecimento com as fórmulas do apêndice para resolvermos esta questão!
Passo 2
Agora é só irmos para o apêndice e encontrarmos as relações para cada uma das componentes. Com isto, teremos o seguinte sistema de equações:
Substituindo os valores corretamente, temos:
Resolvendo o sistema, chegamos a:
E assim descobrimos as primeiras reações.
Passo 3
Já para descobrirmos as outras forças, como o corpo está em equilíbrio, basta analisamos o somatório de forças. Portanto,
Resolvendo o sistema acima, obtemos:
E assim finalizamos a questão!