Seja a superfície parametrizada
(a) Calcule a equação implícita para a imagem de .
(b) Esboce a imagem de .
(c) Justifique se a imagem de é uma superfície regular ou não. Calcule o plano tangente à imagem de no ponto
(d) Calcule a área de
Passo 1
Letra a)
Da equação , pode-se isolar:
Utilizando a relação fundamental da trigonometria e substituindo
e , vamos ter:
Multiplicando por dos dois lados vamos ter
Se isolarmos em , vamos ter a relação:
Substituindo agora na equação :
Essa é a equação implícita que queríamos achar.
Passo 2
Letra b)
Para fazer o esboço, vamos analisar a equação pois existe um macete sempre que temos equações desse tipo, que é uma superfície de revolução.
Pra cada eixo temos uma cara de função parecida
Rotação no eixo :
Rotação no eixo :
Rotação no eixo :
Para o nosso caso é uma rotação no eixo , onde:
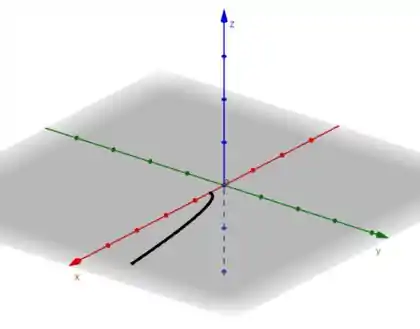
O que temos aqui é somente a parábola , , rotacionando em torno do eixo .
Desenhando ela vamos ter:
Agora rotacionando em torno do eixo :
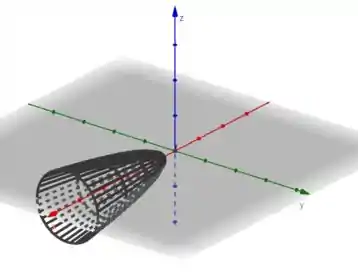
Passo 3
Letra c)
Uma superfície é regular quando temos:
Para todos os pontos do seu domínio.
Vamos começar fazendo as derivadas parciais:
Realizando agora o produto vetorial:
Utilizando a relação fundamental da trigonometria pra organizar nosso vetor normal vamos ter:
Para , vamos ter que , o que indicaria que não é regular, mas o pulo do gato aqui é ver que uma superfície é regular quando pelo menos em alguma parametrização temos a desigualdade
Vamos buscar uma outra parametrização. A equação explícita que obtivemos na letra (a) é uma boa forma de contornarmos isso.
Realizando a parametrização :
Calculando agora o vetor normal para essa parametrização:
Qualquer que seja os valores de e , o vetor normal não zerará, então podemos afirmar que a superfície é regular.
Passo 4
Partindo agora para encontrar plano tangente.
Um plano tangente a uma superfície em um determinado ponto pode ser encontrado fazendo:
Onde e é o vetor normal aplicado nesse ponto.
Pela enunciado, nosso e para descobrirmos quais devem ser o valor de e , substituiremos eles na parametrização da superfície e igualaremos com :
Assim vamos ter que:
Substituindo os valores e realizando a multiplicação na equação para encontrar o plano:
A equação do plano será então:
Passo 5
Letra d)
Como já temos nossa superfície parametrizada, para calcular a área vamos fazer
Onde e para calcular a norma do vetor , vamos fazer:
Substituindo para encontrar a área:
Resolvendo para :
Resolvendo agora para
Nossa área então vai ser:
Resposta
a)
b)
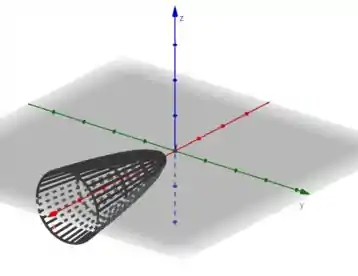
c)
d)