Faça um programa que mostre o apenas o n-ésimo termo da série de Fibonacci. Esse programa deve receber como entrada um número inteiro n maior que 2 (considere que 0 e 1 são conhecidos, sendo eles os 2 primeiros números da série).
Passo 1
Para construirmos esse algoritmo em C precisamos definir o seu escopo de atuação.
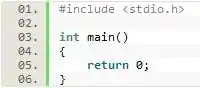
Passo 2
Com o escopo do programa definido, nós podemos declarar e inicializar as variáveis que serão úteis para o desenvolvimento e execução do programa.

A seguir estão algumas informações sobre elas:
- n armazenará o valor da posição de um determinado elemento da série;
- i será uma variável contadora;
- x e y serão responsáveis por armazenar os termos e de todo o processo até o elemento desejado da série, considere o termo atualmente processado pelo programa;
- fibonacci (equivalente a ) armazenará a soma entre e de todo o processo até armazenar o valor de através da soma de e .
Passo 3
Com todas as variáveis declaradas e devidamente inicializadas, nós podemos requisitar a entrada do programa ao usuário.
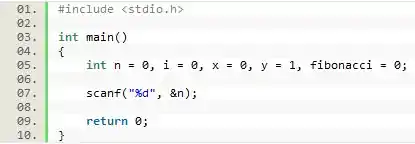
Nesse caso, a entrada do programa será a posição n da série de Fibonacci.
Passo 4
Para realizar o cálculo da sequência, nós podemos utilizar uma estrutura de repetição for com o processamento consecutivo das operações até a obtenção do valor desejado.
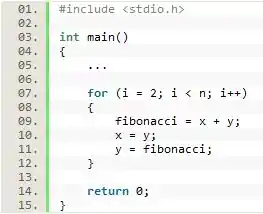
Sendo que a definição dessa estrutura deve ser feita com os seguintes parâmetros:
- i é atribuída com o valor 2 (excluindo os 2 primeiros termos da série que já são conhecidos);
- A condição de execução da estrutura é i menor que n;
- Com o incremento da variável contadora i em uma unidade a cada loop.
A lógica por traz desse laço de repetição está em somar os dois termos anteriores e atribuí-los a variável fibonacci atualizando os mesmos até obtermos o valor de .
Para entendermos melhor o que acontece, considere k o atual termo em processamento pelo laço de repetição. Dessa forma, a cada loop temos a seguinte operação (linha 09), mas como queremos , enquanto os termos que representam os elementos anteriores ao atual devem ser atualizados. Ou seja, se torna (linha 10) e se torna (linha 11) até o momento que obtivermos o elemento da série.
Passo 5
Depois disso tudo, basta imprimirmos o valor presente na variável fibonacci, uma vez que ao término do laço de repetição ela armazenará o elemento da série.
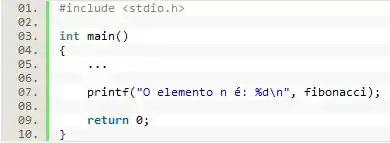
Vale ressaltar que essa impressão será seguida de uma quebra de linha.
Resposta
Ei, a resposta está no passo a passo :)