Considere . Seja a equação diferencial de primeira ordem em , com valor inicial conhecido, .
Resolva a equação diferencial utilizando o SIMULINK.
Passo 1
Para resolver uma equação diferencial pelo SIMULINK, a dica é “isolar” a derivada da EDO. Por isso, vamos rearranjar a EDO para:
Desta forma, conseguimos fazer aquele raciocínio: “a derivada é igual a quê?” e descobrimos onde pôr o bloco “Integrator” para obter . Além do mais, isso ajuda a identificar qual o primeiro bloco que colocaremos no modelo, que muito provavelmente virá da biblioteca “Source”.
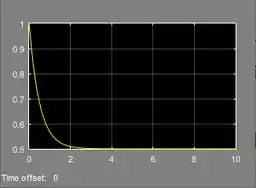
A resposta do exercício será um gráfico de , por isso, usaremos no modelo um bloco “Scope”.
Passo 2
Olhando a EDO rearranjada, sabemos é igual a , por isso, vamos começar modelando essa diferença, o lado direito da equação. Em um novo modelo, insira um bloco “Constant” e faça com que ele seja igual a . Em seguida, insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo), para que ambas as entradas de “Add” tenham um sinal negativo, para fazermos .

Passo 3
O objetivo é que a saída de “Add” seja igual a . E quem é ? É ! Logo, é à direita de “Add” que incluiremos um bloco “Integrator”, que nos dará . Para isto, vá à biblioteca “Continuous”, insira um bloco “Integrator” ao modelo e conecte sua entrada à saída de “Add”, como na figura abaixo:

Não sei se você reparou, mas eu anotei ali no modelo, acima da flecha entre “Add” e “Integrator”, um , pra dizer que aquele sinal é a derivada de . Você pode fazer isso clicando no botão “Annotation” (destacado em azul acima), na lateral esquerda da janela onde construímos os modelos, e em seguida clicando sobre o lugar onde você quer fazer a anotação. Daí, é só digitar o que você quiser.
Esse é um jeito bom de não se perder nos diagramas de blocos das EDOs.
Vamos alterar a condição inicial para , acessando as propriedades de “Integrator” e mudando o parâmetro “Initial Condition” de para :

Passo 4
A saída de “Integrator” será , a solução da nossa EDO. Como queremos gerar o gráfico dela, vamos inserir um bloco “Scope”. Conecte a saída de “Integrator” a entrada de “Scope”:

Agora que temos , podemos criar a componente da expressão . Para isto, insira um bloco “Gain”, da biblioteca “Math Operations”, altere seu ganho para e conecte sua entrada ao sinal saindo de “Integrator”. Você fará isto clicando sobre a entrada de “Gain” e arrastando. Aparecerá um flecha vermelha:
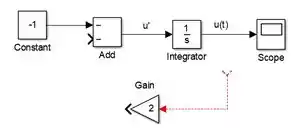
Conecte a extremidade livre à seta entre “Integrator” e “Scope”. Desta forma, vai para “Scope” e “Gain” simultaneamente. Em seguida, conecte a saída de “Gain” à entrada disponível de “Add”. Você estará levando para fazer a diferença :
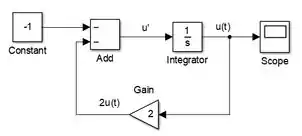
Pronto! A EDO está modelada no SIMULINK e podemos obter sua solução, em forma de gráfico, rodando o programa.
Resposta