Um orifício de borda viva, com tomadas de canto, e um manômetro de coluna de água são usados para medir vazão de ar comprimido. Os seguintes dados são disponíveis:
Diâmetro interno da linha de ar: 150 mm
Diâmetro da placa de orifício: 100 mm
Pressão a montante: 600 kPa
Temperatura do ar 25°C
Deflexão do manômetro 750 mmH2O
Calcule a vazão em volume na linha, expressa em metros cúbicos por hora.
Passo 1
Temos um exercício que pede a vazão (eba! Vamos medir vazão, o objetivo desse tópico! :D) e o instrumento utilizado é placa de orifício.
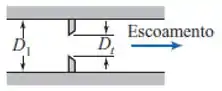
Organizando os dados, temos que:
Diâmetro interno da linha de é o diâmetro antes da medição, logo:
Diâmetro da placa de orifício é Dt
A partir desses dois dados, já podemos calcular β
A temperatura do ar é 25°C, ou seja, 298 K
E o que nos interessa a respeito da pressão aqui é o . Esse é o termo que entra no cálculo da vazão. O enunciado informa que , mas não informa ☹
Mas relaxa! Quando ele diz que a “deflexão do manômetro 750 mmH2O”, ele está falando justamente do ! Só que temos que passar para o sistema internacional, para calcular certinho, com coerência nas unidades
Como a diferença de pressão é bem pequenininha (a pressão atmosférica é da ordem de , por exemplo), podemos considerar esse escoamento de ar incompressível. Mas só por causa disso, ok? 😉
Com isso, conseguimos calcular sua massa específica ρ. Usando pv=nRT
E multiplicando pela massa molar MM do ar, que é 0,02884 kg/mol a 25°C
Substituindo os valores de pressão e Temperatura antes da medição (a montante)
Passo 2
Além dessses dados, o que mais precisamos para calcular a vazão?
Primeiro, vamos reescrever essa área da garganta (At) aí. Atualizando a equação da vazão:
Conhecemos todos os valores, menos o K. Para saber quem ele é, precisamos usar o gráfico de K em relação a Reynolds para a placa de orifício informada.
Quem é Reynolds? Nosso querido e amado
Não temos a velocidade em 1, mas podemos escrever como vazão volumétrica sobre área
O que deixa nosso Reynolds assim
Reynolds, que é quem precisamos saber para achar K e consequentemente encontrar a vazão depende da vazão volumétrica. E aí? Como faz agora?
Aqui mora uma sacada muito boa! Vamos ver o gráfico de K versus Re. Repara que para valores de Reynolds maiores que , para cada curva, o K é praticamente o mesmo!
Cada curva está associada a um β. Nosso β é 0,66. Como não temos essa curva, vamos usar um valor entre as curvas de β =0,6 e 0,7. Assimi, encontramos K = 0,675.
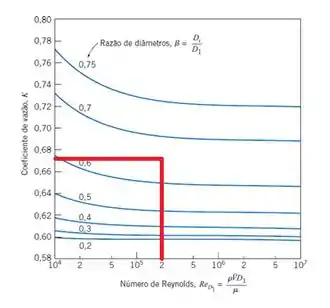
Tá, mas como vamos conferir se esse chute está certo?
Primeiro, vamos calcular a vazão com esse K que veio da hipótese inicial.
Substituindo
Lembrando que
E encontramos essa vazão volumétrica
Passo 3
Para saber se nossa hipótese está certa, vamos utilizar esse valor de Q para calcular o Reynolds. Se der maior que , então acertamos!
Como , então a hipótese está certa e
Como ela está sendo pedida em , vamos converter
Encontramos a vazão volumétrica 😉