Calcule a projeção ortogonal do vetor sobre o espaço gerado por e
(a)
(b)
(c)
(d)
Passo 1
Precisamos projetar um vetor no espaço gerado por e
Esses dois vetores não são LD (um não é múltiplo do outro), logo formam uma base para o espaço.
Mas repara que os dois não são ortogonais entre si, pois produto interno entre eles não é zero.
Então, pra fazer essa projeção, vamos usar os mínimos quadrados!
Por esse método, resolvemos a equação:
onde:
- A é uma matriz cujos vetores das colunas são os vetores da base do espaço em que estamos projetando;
- b é o vetor que queremos projetar/aproximar
- z é a nossa incógnita e é um vetor cujas entradas dão a nossa melhor aproximação para o vetor b
Tá, mas depois de achar z, o problema foi resolvido??
NÃO! Porque queremos a projeção, então vamos ter que fazer ainda:
Agora sim, vamos resolver essa questão!
Passo 2
De acordo com o que vimos antes, temos:
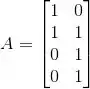
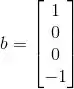
Montando a equação e resolvendo:
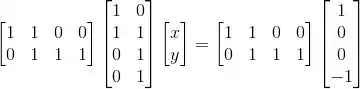
![]()
Vamos resolver esse sistema montando a matriz aumentada e escalonando:
![]()
![]()
Então:
Pela primeira linha:
Logo:
Passo 3
Agora não esquece de fazer a projeção!
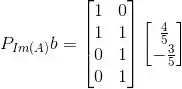
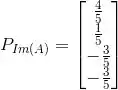
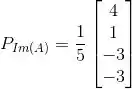
Resposta
(c)