Considere o sistema de equações lineares abaixo:
- Resolva o sistema de equações lineares usando o MATLAB;
- Plote as retas das equações e indique no gráfico a solução encontrada na letra a.
Passo 1
O exercício é dividido em duas partes: na letra a, ele nos pede para resolver um sistema de equações lineares composto por duas equações e duas incógnitas. Para isso, podemos usar qualquer um dos comandos aprendidos na aula: matriz inversa, barra invertida, ou o .
Na letra b, o exercício pede para plotarmos as retas das equações e indicar no gráfico gerado o ponto que representa a solução encontrada na letra a. É possível fazer isso porque podemos manipular as equações do sistema para um formato ou (dá na mesma usar qualquer um dos formatos) e plotar as retas em um plano. O ponto onde as duas retas representanto as equações se encontram, isto é, o ponto de intersecção das duas retas, representa a solução do sistema de equações lineares obtida na letra a.
Passo 2
Vamos começar respondendo a letra a. Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para o sistema:
Temos:
Agora, crie um script novo no MATLAB e digite a matriz e o vetor :

Eu entrei o vetor como um vetor linha e transpus ele, usando a aspas simples (), para ele se tornar um vetor coluna. Mas você pode entrar com da forma que quiser.
Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:

Isto quer dizer que a solução do sistema de equações lineares é e . Esta é a resposta da letra a do exercício.
Passo 4
Vamos responder à letra b, que nos pede para gerar um gráfico com as equações do sistema e, em seguida, indicar no gráfico a solução do sistema obtida na letra a.
A primeira coisa que devemos fazer é dar uma manipulada nas equações, para deixá-las na forma ou . Eu escolhi o formato , mas se quiser o formato , sem problemas, o resultado será o mesmo.
Deixando as equações no formato , temos:
Você pode usar o mesmo script do MATLAB onde você fez a letra a ou criar um novo, tanto faz. Para podermos gerar o gráfico, vamos criar um vetor z indo de a , com um passo igual a , com o comando:
![]()
Em seguida, vamos calcular dois vetores, e , representando as funções acima:
![]()
representa o resultado da função , para cada elemento do vetor . Da mesma forma, representa a função , calculada para cada elemento de .
Passo 5
Após criarmos os vetores e , podemos plotar as retas representando as equações do sistema linear. Para isto, digite os comandos:
![]()
O primeiro comando gera, em um mesmo gráfico, as retas representando e .
O primeiro par dentro do , , representa e indica que está no eixo horizontal do gráfico e que está no eixo vertical do gráfico.
Da mesma forma, o segundo par indica que está no eixo horizontal e que está no eixo vertical e representa .
O segundo comando pede que o gráfico gerado pelo tenha linhas de grade, para facilitar a identificação das coordenadas dos pontos das retas.
Ao rodarmos o programa, temos este gráfico:
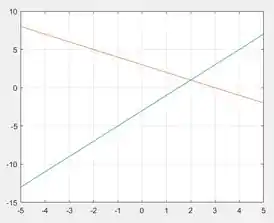
A reta azul representa e a reta vermelha, .
Para indicar no gráfico a solução da letra a, clique no ponto onde as retas se encontram. Veja pelas linhas de garde que elas se interceptam bem em . O MATLAB mostrará as coordenadas do ponto onde você clicou. As coordenadas do ponto de intersecção das retas são a solução do sistema de equações lineares do exercício.
Resposta
- A solução do sistema de equações lineares é e .
- O gráfico abaixo apresenta as retas representando as equações do sistema:

As coordenadas do ponto de intersecção, apresentado no gráfico, representam a solução encontrada na letra a.