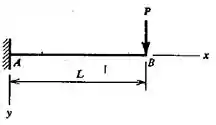
Deduzir a equação da linha elástica de uma viga em balanço, com uma concentrada na extremidade livre (ver a figura). Calcular, também, a deflexão e o deslocamento angular na mesma extremidade.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a equação da linha elástica, como também a deflexão e deslocamento angular na extremidade livre, para uma viga engastada submetida a uma carga pontual na extremidade livre
Para que a gente consiga resolver a questão, vamos ter que obter o momento fletor para uma seção da viga. Sendo assim, ao fazermos um corte nela, temos o seguinte diagrama de corpo livre:

Então, a partir das equações de equilíbrio, temos que , sendo .
Só que a gente tem um pequeno probleminha: a coordenada usada na questão é , e não (que cresce da direita para esquerda). Fazendo uma mudança de coordenadas, temos:
E agora sim já temos a base para seguirmos com a questão!
Passo 2
Agora que a gente já conhece o momento fletor, vamos ter que fazer integrações sucessivas para obter a equação da linha elástica.
Portanto, utilizando a relação da linha elástica com o momento fletor, temos:
Integrando-a, temos:
Para que a gente termine de determinar a equação da linha elástica, precisamos aplicar as condições de contorno do problema. Neste caso, temos . Portanto,
E assim, chegamos na seguinte equação da linha elástica:
Passo 3
Para finalizarmos a questão, temos que descobrir a equação da deflexão e do deslocamento angular em . Portanto, a deflexão será:
Já o deslocamento angular será:
E assim finalizamos a questão!